题目内容
设函数f(x)=|x+1|+|x+2|-a(a∈R)
(1)当a=5时,求函数g(x)=lnf(x)的定义域;
(2)若函数h(x)=
的定义域为R,试求a的取值范围.
(1)当a=5时,求函数g(x)=lnf(x)的定义域;
(2)若函数h(x)=
| f(x) |
考点:函数的定义域及其求法
专题:计算题,分类讨论,函数的性质及应用
分析:(1)由于对数的真数必须大于0,则有|x+1|+|x+2|-5>0,讨论当x≤-2时,当x≥-1时,当-2<x<-1时,去掉绝对值,解出不等式,最后求并集即可;
(2)函数h(x)=
的定义域为R,则f(x)≥0恒成立,即有|x+1|+|x+2|≥a恒成立,只需a≤(|x+1|+|x+2|)min,运用绝对值不等式的性质,即可得到最小值,进而得到a的范围.
(2)函数h(x)=
| f(x) |
解答:
解:(1)当a=5时,f(x)=|x+1|+|x+2|-5,
g(x)=lnf(x)=ln(|x+1|+|x+2|-5),
即有|x+1|+|x+2|-5>0,
当x≤-2时,-x-1-x-2-5>0,即x<-4,则有x<-4;
当x≥-1时,x+1+x+2-5>0,即x>1,则有x>1;
当-2<x<-1时,-x-1+x+2-5>0,即-4>0,则x无解.
故x>1或x<-4.
故函数g(x)的定义域为(-∞,-4)∪(1,+∞);
(2)由于函数h(x)=
的定义域为R,
则f(x)≥0恒成立,
即有|x+1|+|x+2|≥a恒成立,
只需a≤(|x+1|+|x+2|)min,
由于|x+1|+|x+2|≥|(x+1)-(x+2)|=1,
则有a≤1.
故a的取值范围是(-∞,1].
g(x)=lnf(x)=ln(|x+1|+|x+2|-5),
即有|x+1|+|x+2|-5>0,
当x≤-2时,-x-1-x-2-5>0,即x<-4,则有x<-4;
当x≥-1时,x+1+x+2-5>0,即x>1,则有x>1;
当-2<x<-1时,-x-1+x+2-5>0,即-4>0,则x无解.
故x>1或x<-4.
故函数g(x)的定义域为(-∞,-4)∪(1,+∞);
(2)由于函数h(x)=
| f(x) |
则f(x)≥0恒成立,
即有|x+1|+|x+2|≥a恒成立,
只需a≤(|x+1|+|x+2|)min,
由于|x+1|+|x+2|≥|(x+1)-(x+2)|=1,
则有a≤1.
故a的取值范围是(-∞,1].
点评:本题考查函数的定义域的求法,注意对数的真数必须大于0,偶次根式被开方式非负,同时考查绝对值不等式的性质,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
复数
=( )
| 2 |
| 1-i |
| A、1+i | B、1-i |
| C、i | D、1-2i |
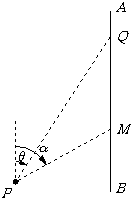 如图,P为某湖中观光岛屿,AB是沿湖岸南北方向道路,Q为停车场,PQ=
如图,P为某湖中观光岛屿,AB是沿湖岸南北方向道路,Q为停车场,PQ=