题目内容
已知圆C1:x2+y2-2x=0与圆C2:x2+y2+4y=0交于点A、B,则直线AB的方程为 .
考点:相交弦所在直线的方程
专题:计算题,直线与圆
分析:要求两圆的公共弦方程,可将两圆方程相减即可得到所求方程.
解答:
解:圆C1:x2+y2-2x=0与圆C2:x2+y2+4y=0交于A,B两点,
则可将两圆方程相减得,x2+y2-2x-(x2+y2+4y)=0,
即2x+4y=0,即有x+2y=0,
即为直线AB的方程.
故答案为:x+2y=0.
则可将两圆方程相减得,x2+y2-2x-(x2+y2+4y)=0,
即2x+4y=0,即有x+2y=0,
即为直线AB的方程.
故答案为:x+2y=0.
点评:本题考查的知识点是圆与圆的位置关系,直线与圆的位置关系,其中将两个圆方程相减,直接得到公共弦AB的方程可以简化解题过程.

练习册系列答案
相关题目
半径为R的球内接一个正方体,则该正方体的体积是( )
A、
| ||||
B、
| ||||
C、2
| ||||
| D、8R3 |
已知点 P为双曲线
-
=1右支上一点,点F1,F2分别为双曲线的左、右焦点,M为△PF1F2的内心,若S△PMF1=S△PMF2+8,则△MF1F2的面积为( )
| x2 |
| 16 |
| y2 |
| 9 |
A、2
| ||
| B、10 | ||
| C、8 | ||
| D、6 |
已知幂函数y=f(x)的图象过点(3,
),则f(9)=( )
| 3 |
| A、3 | ||
| B、-3 | ||
C、-
| ||
D、
|
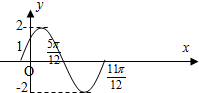 已知函数f(x)=Asin(ωx+φ)(A>0,w>0,|φ|<π)在一个周期内的图象如下图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,w>0,|φ|<π)在一个周期内的图象如下图所示.