题目内容
14.$\frac{sin(-340°)sin70°}{co{s}^{2}155°-si{n}^{2}25°}$的值是$\frac{1}{2}$.分析 直接利用诱导公式及倍角公式化简求值.
解答 解:$\frac{sin(-340°)sin70°}{co{s}^{2}155°-si{n}^{2}25°}$=$\frac{sin(-360°+20°)cos20°}{co{s}^{2}25°-si{n}^{2}25°}$
=$\frac{sin20°cos20°}{cos50°}=\frac{2sin20°cos20°}{2cos50°}$=$\frac{sin40°}{2sin40°}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查三角函数的化简求值,考查了倍角公式及诱导公式的应用,是基础的计算题.

练习册系列答案
相关题目
5.已知数列{an}前n项和满足Sn-Sn-1=$\sqrt{{S}_{n}}$+$\sqrt{{S}_{n-1}}$ (n≥2),a1=1,则an=( )
| A. | n | B. | 2n-1 | C. | n2 | D. | 2n2-1 |
2.已知函数f(x)=($\frac{1}{3}$)x,a>0,b>0,a≠b,m=f($\frac{a+b}{2}$),n=f($\sqrt{ab}$),p=f($\frac{2ab}{a+b}$),则m,n,p 的大小关系为( )
| A. | m<n<p | B. | m<p<n | C. | p<m<n | D. | p<n<m |
9.$\sqrt{si{n}^{2}480°}$等于( )
| A. | ±$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
3.已知向量$\overrightarrow{a}$=(cosθ,sinθ),θ∈(0,π),$\overrightarrow{b}$=(1,$\sqrt{3}$),若$\overrightarrow{a}$与$\overrightarrow{b}$共线,则sin2θ=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
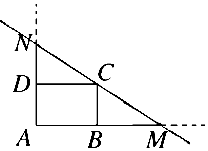 如图,已知矩形ABCD中,AB=6,AD=4,过点C的直线l与AB,AD的延长线分别交于点M,N.
如图,已知矩形ABCD中,AB=6,AD=4,过点C的直线l与AB,AD的延长线分别交于点M,N.