题目内容
在一次考试中,由于不慎,致使一选择题已知条件被黑色墨水覆盖,原题为:已知α、β均为锐角,且sinα-sinβ=-
, ,则tan(α-β)的值为 A.
B.
C.-
D.-
其中 为覆盖部分,试根据所附答案为C,推断并补出被覆盖部分.
| 1 |
| 2 |
| ||
| 3 |
| 3 | ||
|
| ||
| 3 |
| 3 | ||
|
其中
考点:两角和与差的正切函数,两角和与差的正弦函数
专题:三角函数的求值
分析:逆推:根据所附答案可得tan(α-β)=-
,可得sinα-sinβ=sin[(α-β)+β]-sin[α-(α-β)]=-
,由两角和与差得正弦展开并整理,又角的范围和同角三角函数的基本关系可求cos(α-β)和sin(α-β)的值,代入可解cosα+cosβ=-
,可得答案.
| ||
| 3 |
| 1 |
| 2 |
3
| ||
| 14 |
解答:
解:根据所附答案为C,可得tan(α-β)=-
,
又sinα-sinβ=-
,∴sin[(α-β)+β]-sin[α-(α-β)]=-
,
由两角和与差得正弦展开并整理可得(sinβ-sinα)cos(α-β)+(cosα+cosβ)sin(α-β)=0,(*)
∵α、β均为锐角,∴-
<α-β<
,又tan(α-β)=-
<0,∴-
<α-β<0,
∴cos(α-β)=
,sin(α-β)=-
,
代入(*)式可得-
×
-
(cosα+cosβ)=0,
解得cosα+cosβ=-
故答案为:cosα+cosβ=-
| ||
| 3 |
又sinα-sinβ=-
| 1 |
| 2 |
| 1 |
| 2 |
由两角和与差得正弦展开并整理可得(sinβ-sinα)cos(α-β)+(cosα+cosβ)sin(α-β)=0,(*)
∵α、β均为锐角,∴-
| π |
| 2 |
| π |
| 2 |
| ||
| 3 |
| π |
| 2 |
∴cos(α-β)=
| 3 |
| 4 |
| ||
| 4 |
代入(*)式可得-
| 1 |
| 2 |
| 3 |
| 4 |
| ||
| 4 |
解得cosα+cosβ=-
3
| ||
| 14 |
故答案为:cosα+cosβ=-
3
| ||
| 14 |
点评:本题考查三角函数公式,涉及分析法推理,属中档题.

练习册系列答案
相关题目
 如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连接AE,AF结分别与CD交于G,H.
如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连接AE,AF结分别与CD交于G,H.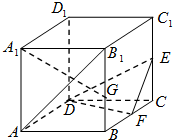 如图,已知正方体AC1棱长为2,E、F、G分别是CC1、BC和CD的中点.
如图,已知正方体AC1棱长为2,E、F、G分别是CC1、BC和CD的中点.