题目内容
已知sinθ、cosθ是关于x的方程x2-ax+a=0(a∈R)的两个根.
(1)求cos(
-θ)+sin(
+θ)的值;
(2)求tan(π-θ)-
的值.?
(1)求cos(
| π |
| 2 |
| π |
| 2 |
(2)求tan(π-θ)-
| 1 |
| tanθ |
考点:三角函数的化简求值
专题:三角函数的求值
分析:由△≥0可得a的范围,由韦达定理和同角三角函数的基本关系可得a的方程,可得sin θ+cos θ=sin θcos θ=1-
.
(1)由诱导公式可得cos(
-θ)+sin(
+θ)=sin θ+cos θ,
(2)化简可得原式=-
,代入可得.
| 2 |
(1)由诱导公式可得cos(
| π |
| 2 |
| π |
| 2 |
(2)化简可得原式=-
| 1 |
| sinθcosθ |
解答:
解:由已知原方程判别式△=(-a)2-4a≥0,
解得a≥4或a≤0.又
∴(sin θ+cos θ)2=1+2sin θcos θ,即a2-2a-1=0.
∴a=1-
或a=1+
(舍去).
∴sin θ+cos θ=sin θcos θ=1-
.
(1)由诱导公式可得cos(
-θ)+sin(
+θ)=sin θ+cos θ=1-
.
(2)tan(π-θ)-
=-tan θ-
=-(tanθ+
)=-(
+
)
=-
=-
=
+1.
解得a≥4或a≤0.又
|
∴(sin θ+cos θ)2=1+2sin θcos θ,即a2-2a-1=0.
∴a=1-
| 2 |
| 2 |
∴sin θ+cos θ=sin θcos θ=1-
| 2 |
(1)由诱导公式可得cos(
| π |
| 2 |
| π |
| 2 |
| 2 |
(2)tan(π-θ)-
| 1 |
| tanθ |
| 1 |
| tanθ |
=-(tanθ+
| 1 |
| tanθ |
| sinθ |
| cosθ |
| cosθ |
| sinθ |
=-
| 1 |
| sinθcosθ |
| 1 | ||
1-
|
| 2 |
点评:本题考查三角函数求值,涉及韦达定理的应用,属中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
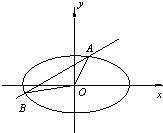 直线y=kx+b与曲线x2+4y2-4=0交于A、B两点,记△AOB的面积为S(O是坐标原点).
直线y=kx+b与曲线x2+4y2-4=0交于A、B两点,记△AOB的面积为S(O是坐标原点). 如图,在△ABC中,A(2,4),B(-1,-2),C(4,3),BC边上的高为AD
如图,在△ABC中,A(2,4),B(-1,-2),C(4,3),BC边上的高为AD