题目内容
已知函数f(x)=x3+2bx2+cx+1有两个极值点x1、x2,且x1∈[-2,-1],x2∈[1,2],则f(-1)的取值范围是 ( )
| A.[-,3] | B.[,6] | C.[3,12] | D.[-,12] |
C
试题分析:
 ,即
,即 的两根满足x1∈[-2,-1],x2∈[1,2],即
的两根满足x1∈[-2,-1],x2∈[1,2],即 ,即
,即 ,画出平面区域,可得
,画出平面区域,可得 过点(0,-12)时取最大值12,过点(0,-3)时取最小值3,选C.
过点(0,-12)时取最大值12,过点(0,-3)时取最小值3,选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值; 的单调区间.
的单调区间.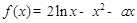 .
.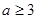 时,讨论函数
时,讨论函数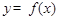 在[
在[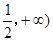 上的单调性;
上的单调性;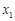 ,
,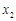
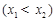 是函数
是函数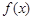 的两个零点,
的两个零点,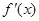 为函数
为函数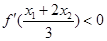 .
.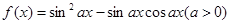 的图象与直线
的图象与直线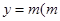 为常数)相切,并且切点的横坐标依次成等差数列,且公差为
为常数)相切,并且切点的横坐标依次成等差数列,且公差为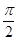
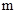 的值;
的值; 是
是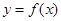 图象的对称中心,且
图象的对称中心,且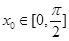 ,求点A的坐标
,求点A的坐标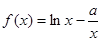 (
(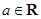 ).
).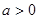 时,判断
时,判断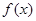 在定义域上的单调性;
在定义域上的单调性;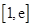 上的最小值为
上的最小值为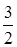 ,求
,求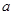 的值;
的值;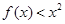 在
在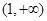 上恒成立,试求
上恒成立,试求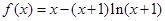 (
(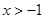 ).
).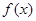 的单调区间;
的单调区间;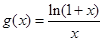 (
(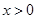 )的单调性证明:当
)的单调性证明:当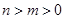 时,
时,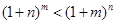 ;
;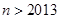 ,且
,且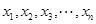 均为正实数,
均为正实数, 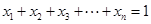 时,
时,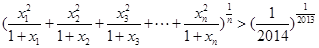 .
.
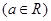 .
.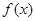 在
在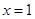 处的切线垂直于直线
处的切线垂直于直线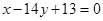 ,求该点的切线方程,并求此时函数
,求该点的切线方程,并求此时函数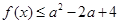 对任意的
对任意的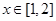 恒成立,求实数
恒成立,求实数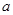 的取值范围.
的取值范围.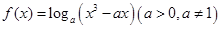 在区间
在区间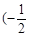 ,0)内单调递增,则
,0)内单调递增,则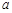 取值范围是( )
取值范围是( )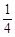 ,1)
,1)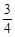 ,1)
,1)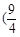 ,
,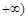
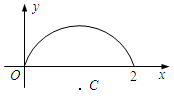
 )
)
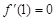 ;②
;②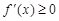 ;③
;③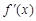 为减函数;④若
为减函数;④若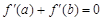 ,则a+b=2.
,则a+b=2.