题目内容
设函数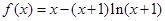 (
(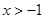 ).
).
(Ⅰ)求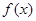 的单调区间;
的单调区间;
(Ⅱ)试通过研究函数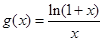 (
(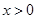 )的单调性证明:当
)的单调性证明:当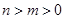 时,
时,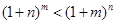 ;
;
(Ⅲ)证明:当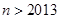 ,且
,且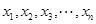 均为正实数,
均为正实数, 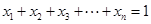 时,
时,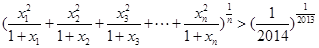 .
.
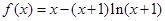 (
(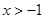 ).
).(Ⅰ)求
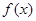 的单调区间;
的单调区间;(Ⅱ)试通过研究函数
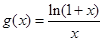 (
(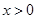 )的单调性证明:当
)的单调性证明:当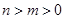 时,
时,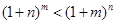 ;
;(Ⅲ)证明:当
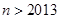 ,且
,且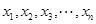 均为正实数,
均为正实数, 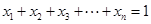 时,
时,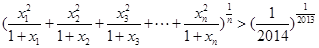 .
.(1)单调递增区间为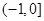 ,单调递减区间为
,单调递减区间为 ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析.
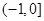 ,单调递减区间为
,单调递减区间为 ;(2)证明过程详见解析;(3)证明过程详见解析.
;(2)证明过程详见解析;(3)证明过程详见解析.试题分析:(1)求导数,讨论真数与1的大小来判断
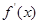 的正负;(2)利用函数的单调性证明大小关系;(3)利用柯西不等式列出不等式,两边取
的正负;(2)利用函数的单调性证明大小关系;(3)利用柯西不等式列出不等式,两边取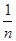 幂,两边去倒数,利用不等式的性质证明.
幂,两边去倒数,利用不等式的性质证明.试题解析:(Ⅰ)由
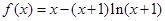 ,有
,有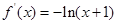 , 1分
, 1分当
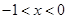 ,即
,即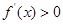 时,
时,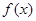 单调递增;
单调递增;当
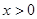 ,即
,即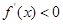 时,
时,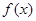 单调递减;
单调递减;所以
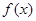 的单调递增区间为
的单调递增区间为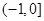 ,单调递减区间为
,单调递减区间为 . 3分
. 3分(Ⅱ)设
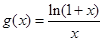 (
(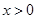 ),则
),则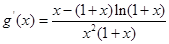 ,5分
,5分由(Ⅰ)知
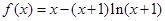 在
在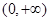 单调递减,且
单调递减,且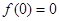 ,
,∴
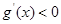 在
在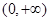 恒成立,故
恒成立,故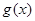 在
在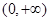 单调递减,
单调递减,又
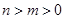 ,∴
,∴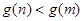 ,得
,得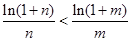 ,
,∴
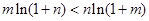 ,即:
,即: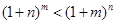 .8分
.8分(Ⅲ)由
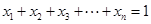 ,及柯西不等式:
,及柯西不等式: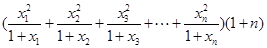
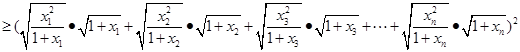
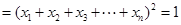 ,
, 所以
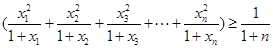 ,
,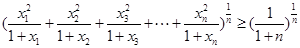 . 11分
. 11分又
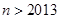 ,由(Ⅱ)可知
,由(Ⅱ)可知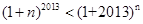 ,
,即
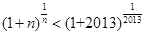 ,即
,即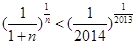 .
.则
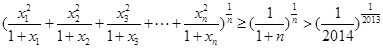 .
.故
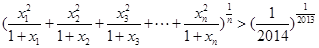 . 14分
. 14分 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
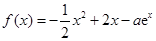 .
.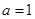 ,求
,求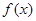 在
在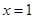 处的切线方程;
处的切线方程;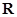 上是增函数,求实数
上是增函数,求实数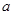 的取值范围.
的取值范围.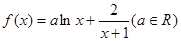 .
.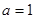 时,求
时,求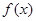 在
在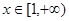 最小值;
最小值;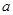 的取值范围;
的取值范围;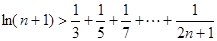 (
(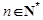 ).
).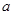 、
、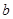 、
、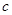 都是实数,函数
都是实数,函数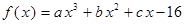 的导函数为
的导函数为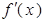 ,
,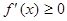 的解集为
的解集为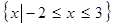 .
.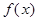 的极大值等于
的极大值等于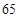 ,求
,求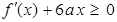 的解集为集合
的解集为集合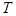 ,当
,当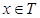 时,函数
时,函数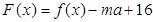 只有一个零点,求实数
只有一个零点,求实数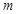 的取值范围.
的取值范围.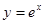 上,点Q在曲线
上,点Q在曲线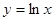 上,则|PQ|最小值为( )
上,则|PQ|最小值为( )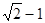

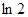
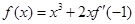 ,则函数
,则函数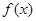 在区间
在区间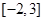 上的值域是_____________.
上的值域是_____________.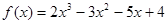 的导数
的导数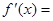 ,
,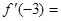
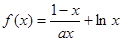 的导函数是
的导函数是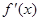 ,则
,则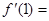 .
.