题目内容
若P点在△ABC确定的平面上,O为平面外一点,下列说法中不正确的是( )
A、
| ||||||||||||||
B、若
| ||||||||||||||
C、
| ||||||||||||||
D、若P点是△ABC的重心,则
|
考点:空间向量的基本定理及其意义
专题:空间向量及应用
分析:A.
、
、
是不共面向量;
B.由于P点在面OAB上,由共面向量定理可得正确;
C.由于P点在△ABC确定的平面上,可知
、
、
是共面向量;
D.利用重心定理即可判断出.
| OA |
| OB |
| OC |
B.由于P点在面OAB上,由共面向量定理可得正确;
C.由于P点在△ABC确定的平面上,可知
| AP |
| AB |
| AC |
D.利用重心定理即可判断出.
解答:
解:A.
、
、
是不共面向量,因此不正确;
B.若
=x
+y
,则P点在面OAB上,由共面向量定理可得正确;
C.∵P点在△ABC确定的平面上,∴
、
、
是共面向量,正确;
D.∵P点是△ABC的重心,则
=
+
+
,正确.
综上可得:只有A不正确.
故选:A.
| OA |
| OB |
| OC |
B.若
| OP |
| OA |
| OB |
C.∵P点在△ABC确定的平面上,∴
| AP |
| AB |
| AC |
D.∵P点是△ABC的重心,则
| OP |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 3 |
| OC |
综上可得:只有A不正确.
故选:A.
点评:本题考查了向量共面定理、重心定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线y=xn(n∈N)在点P(
,2
)处切线斜率为20,那么n为( )
| 2 |
| n |
| 2 |
| A、7 | B、6 | C、5 | D、4 |
y=x(1-3x),(0<x<
)的最大值是( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知Sn=1+
+
+…+
,则Sn等于( )
| 3 |
| 2 |
| 5 |
| 22 |
| 2n-1 |
| 2n-1 |
A、5-
| ||
B、4-
| ||
C、3-
| ||
D、6-
|
将容量为100的样本数据,按从大到小的顺序分成8个组,如表:
则第6组的频率为( )
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 | 11 | 14 | 12 | 13 | 13 | x | 12 | 10 |
| A、0.14 | B、14 |
| C、0.15 | D、15 |
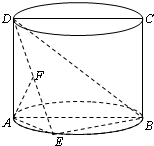 如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上(点E异于A、B两点),点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.
如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上(点E异于A、B两点),点F在DE上,且AF⊥DE,若圆柱的底面积与△ABE的面积之比等于π.