题目内容
17.已知数列{an}满足an+1=2an+3•2n,a1=2,则数列{an}的通项公式是(3n-1)•2n-1.分析 通过对an+1=2an+3•2n两边同时除以2n,从而构造出首项为2、公差为3的等差数列{$\frac{{a}_{n}}{{2}^{n-1}}$},进而计算可得结论.
解答 解:∵an+1=2an+3•2n,
∴$\frac{{a}_{n+1}}{{2}^{n}}$=$\frac{{a}_{n}}{{2}^{n-1}}$+3,
又∵$\frac{{a}_{1}}{{2}^{1-1}}$=2,
∴数列{$\frac{{a}_{n}}{{2}^{n-1}}$}是首项为2、公差为3的等差数列,
∴$\frac{{a}_{n}}{{2}^{n-1}}$=2+3(n-1)=3n-1,an=(3n-1)•2n-1,
故答案为:(3n-1)•2n-1.
点评 本题考查数列的递推式,构造等差数列是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
7.运行图所示的程序,则输出的结果为( )


| A. | 23 | B. | 21 | C. | 19 | D. | 17 |
12.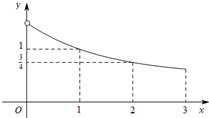 函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
 函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )| A. | [-3,-2]∪[2,3] | B. | [-3,-2]∪(0,1] | C. | [-2,0)∪[1,3] | D. | [-1,0)∪(0,1] |
9.若将函数f(x)=sin2x+cos2x的图象向右平移φ(φ>0)个单位,所得图象关于原点对称,则φ的最小值为( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{3π}{4}$ |
6.已知p:“直线l的倾斜角α=$\frac{π}{4}$”;q:“直线l的斜率k=1”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |