题目内容
1.某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B若干件,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:| 每件产品A | 每件产品B | ||
| 研制成本、搭载费用之和(百万元) | 2 | 1.5 | 计划最大资金额15(百万元) |
| 产品重量(千克) | 1 | 1.5 | 最大搭载重量12(千克) |
| 预计收益(百元) | 1000 | 1200 | 10200(百元) |
分析 设搭载A产品x件,B产品y件,则预计收益z=1000x+1200y.由图表列出关于x,y的不等式组,画出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:设搭载A产品x件,B产品y件,则预计收益z=1000x+1200y.
则有$\left\{\begin{array}{l}2x+1.5y≤15\\ x+1.5y≤12\\ 2x-y≥0\\ x≥0,y≥0\end{array}\right.$.
作出可行域如图: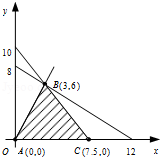
作直线l:1000x+1200y=0,即直线x+1.2y=0.
把直线l向右上方平移到l1的位置,直线l1经过可行域上的点B,
此时z=1000x+1200y取得最大值.
由$\left\{\begin{array}{l}{x-2y=0}\\{2x+1.5y=15}\end{array}\right.$,解得点M的坐标为(3,6).
∴当x=3,y=6时,zmax=3×1000+6×1200=10200(百元).
答:搭载A产品3件,B产品6件,才能使总预计收益达到最大,最大预计收益为10200百元.
故答案为:10200百元.
点评 本题考查简单的线性规划,考查了简单的数学建模思想方法和数形结合的解题思想方法,考查了学生读取图表的能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.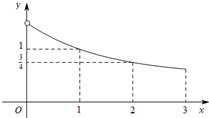 函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
 函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )
函数f(x) 是定义在[-3,0)∪(0,3]上的奇函数,当x∈(0,3]时,f(x) 的图象如图所示,那么满足不等式f(x)≥2x-1 的x的取值范围是( )| A. | [-3,-2]∪[2,3] | B. | [-3,-2]∪(0,1] | C. | [-2,0)∪[1,3] | D. | [-1,0)∪(0,1] |
9.若将函数f(x)=sin2x+cos2x的图象向右平移φ(φ>0)个单位,所得图象关于原点对称,则φ的最小值为( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{3π}{4}$ |
16.已知复数z满足z=$\frac{1}{1+i}$(i为虚数单位),则z=( )
| A. | $\frac{1-i}{2}$ | B. | $\frac{1+i}{2}$ | C. | 1-i | D. | 1+i |
6.已知p:“直线l的倾斜角α=$\frac{π}{4}$”;q:“直线l的斜率k=1”,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |