题目内容
若直线2ax+by-2=0(a,b∈R*)平分圆x2+y2-2x-4y-6=0,则
+
的最小值是 .
| 2 |
| a |
| 1 |
| b |
考点:基本不等式,直线与圆的位置关系
专题:不等式的解法及应用
分析:直线2ax+by-2=0(a,b∈R*)平分圆x2+y2-2x-4y-6=0,可得:直线2ax+by-2=0(a,b∈R*)经过圆心,于是a+b=1.再利用“乘1法”与基本不等式的性质即可得出.
解答:
解:圆x2+y2-2x-4y-6=0化为(x-1)2+(y-2)2=11,圆心为C(1,2),
∵直线2ax+by-2=0(a,b∈R*)平分圆x2+y2-2x-4y-6=0,
∴直线2ax+by-2=0(a,b∈R*)经过圆心C(1,2),
∴2a+2b-2=0,化为a+b=1.
∴
+
=(a+b)(
+
)=3+
+
≥3+2
=3+2
,当且仅当a=
b=2-
时取等号.
∴
+
的最小值是3+2
.
故答案为:3+2
.
∵直线2ax+by-2=0(a,b∈R*)平分圆x2+y2-2x-4y-6=0,
∴直线2ax+by-2=0(a,b∈R*)经过圆心C(1,2),
∴2a+2b-2=0,化为a+b=1.
∴
| 2 |
| a |
| 1 |
| b |
| 2 |
| a |
| 1 |
| b |
| 2b |
| a |
| a |
| b |
|
| 2 |
| 2 |
| 2 |
∴
| 2 |
| a |
| 1 |
| b |
| 2 |
故答案为:3+2
| 2 |
点评:本题考查了圆的性质、“乘1法”与基本不等式的性质,属于基础题.

练习册系列答案
相关题目
设a=sin13°+cos 13°,b=2
cos214°-
,c=
,则a,b,c的大小关系为( )
| 2 |
| 2 |
| ||
| 2 |
| A、b<c<a |
| B、a<c<b |
| C、c<a<b |
| D、c<b<a |
已知a、b、c满足c<b<a,且ac<0,那么下列选项中一定不成立的( )
| A、ab>ac |
| B、c(b-a)<0 |
| C、cb2≤ab2 |
| D、ac(a-c)<0 |
不等式
>2的解集为( )
| x-1 |
| x-3 |
| A、{x|x<1} |
| B、{x|x>3} |
| C、{x|x<3或x>5} |
| D、{x|3<x<5} |
设等差数列{an}的前n项和为Sn,已知a1=-11,a3+a7=-6,当Sn取得最小值是,n=( )
| A、5 | B、6 | C、7 | D、8 |
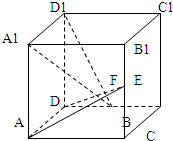 如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.
如果正方体ABCD-A1B1C1D1中EF分别是BB1、CD中点.