题目内容
已知复数z1=sin2x+λi,z2=m+(m-
cos2x)i(λ,m,x∈R),且z1=z2.
(1)设λ=f(x),求f(x)的最小正周期和单调递增区间.
(2)当x∈[0,
]时,求函数f(x)的值域.
| 3 |
(1)设λ=f(x),求f(x)的最小正周期和单调递增区间.
(2)当x∈[0,
| π |
| 2 |
考点:复合三角函数的单调性,复数相等的充要条件,两角和与差的正弦函数
专题:三角函数的求值
分析:(1)通过复数的相等消去m,求出λ的表达式利用两角和与差的三角函数,化简函数为一个角的一个三角函数的形式,求出函数的周期,利用正弦函数的单调增区间求解函数的单调增区间即可.
(2)通过函数的表达式求出相位的范围,利用正弦函数的值域求解函数的值域即可.
(2)通过函数的表达式求出相位的范围,利用正弦函数的值域求解函数的值域即可.
解答:
解:(1)z1=z2⇒
…(1分)
⇒λ=sin2x-
cos2x=2sin(2x-
),…(3分)
所以函数f(x)的最小正周期为
=π,…(4分)
因为2x-
∈[2kπ-
,2kπ+
],k∈Z…(5分)
所以f(x)的单调递增区间为[2kπ-
,2kπ+
],k∈Z.(单调区间写成开区间不扣分)…(6分)
(2)当x∈[0,
]时,2x-
∈[-
,
],…(7分)
所以sin(2x-
)∈[-
,1],…(11分)
因此函数f(x)的值域为[-
,2].…(12分)
|
⇒λ=sin2x-
| 3 |
| π |
| 3 |
所以函数f(x)的最小正周期为
| 2π |
| 2 |
因为2x-
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
所以f(x)的单调递增区间为[2kπ-
| π |
| 12 |
| 5π |
| 12 |
(2)当x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
所以sin(2x-
| π |
| 3 |
| ||
| 2 |
因此函数f(x)的值域为[-
| 3 |
点评:本题考查两角和与差的三角函数,复数相等,正弦函数的单调性周期的求法,考查计算能力.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
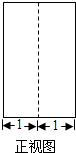 三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则该三棱柱左视图的面积为( )
三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图所示)的面积为8,则该三棱柱左视图的面积为( )A、2
| ||||
B、
| ||||
C、4
| ||||
D、8
|
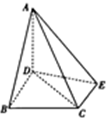 在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2
在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2