题目内容
2．已知1≤a≤3，若f（x）=x2-2ax+1在区间[1，3]上的最大值为M（a），最小值为N（a），令g（a）=M（a）-N（a）．（1）求g（a）的函数表达式；（2）求出g（a）的最小值与最大值．
分析 配方法化简f（x）=x2-2ax+1=（x-a）2+1-a2，从而根据二次函数的性质讨论写出g（a）的表达式，再分类讨论求最值．
解答 解：f（x）=x2-2ax+1=（x-a）2+1-a2，
（1）由二次函数的性质可得，
N（a）=f（a）=1-a2，
当1≤a≤2时，M（a）=f（3）=10-6a，
当2＜a≤3时，M（a）=f（1）=2-2a，
故g（a）=M（a）-N（a）=$\left\{\begin{array}{l}{（a-3）^{2}，1≤a≤2}\\{（a-1）^{2}，2＜a≤3}\end{array}\right.$，
（2）由（1）知，当1≤a≤2时，1≤g（a）≤4；
当2＜a≤3时，1＜g（a）≤4；
故g（a）的最大值为4，最小值为1．
点评 本题考查了二次函数的性质的判断与应用，同时考查了分类讨论的思想应用，属于中档题．
练习册系列答案
相关题目
10．
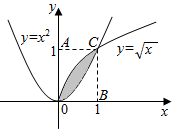由曲线y=x2和曲线y=$\sqrt{x}$围成的一个叶形图如图所示，则图中阴影部分面积为（ ）
由曲线y=x2和曲线y=$\sqrt{x}$围成的一个叶形图如图所示，则图中阴影部分面积为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{3}{10}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |