题目内容
各项均为正数的数列{an}的前n项和Sn满足2Sn=an2+an(n∈N*),等比数列{bn}满足b1=
,bn+1+bn=
(n∈N*).
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)若i,j为正整数,且1≤i≤j≤n,求所有可能的乘积aibj的和.
| 1 |
| 2 |
| 3 |
| 2n+1 |
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)若i,j为正整数,且1≤i≤j≤n,求所有可能的乘积aibj的和.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(I)利用“n=1时,a1=S1;n≥2时,an=Sn-Sn-1”即可化为(an+an-1)(an-an-1-1)=0,an>0可得∴an-an-1=1.利用等差数列的通项公式即可得出.根据等比数列{bn}满足b1=
,bn+1+bn=
(n∈N*).
设公比为q,可得
q+
=
,即可得出.
(II)i,j为正整数,且1≤i≤j≤n,所有可能的乘积aibj的和=a1
bj+a2
bk+…+an-1
bn-1+anbn,化简利用等比数列的前n项和公式、“错位相减法”即可得出.
| 1 |
| 2 |
| 3 |
| 2n+1 |
设公比为q,可得
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
(II)i,j为正整数,且1≤i≤j≤n,所有可能的乘积aibj的和=a1
| n |
 |
| j=1 |
| n |
 |
| k=2 |
| n |
 |
| l=n-1 |
解答:
解:(I)∵各项均为正数的数列{an}的前n项和Sn满足2Sn=an2+an(n∈N*),
∴n=1时,2a1=
+a1,解得a1=1.
当n≥2时,2an=2(Sn-Sn-1)=an2+an-(
+an-1),
化为(an+an-1)(an-an-1-1)=0,
∴an-an-1=1.
∴数列{an}是等差数列,
∴an=1+(n-1)×1=n.
∵等比数列{bn}满足b1=
,bn+1+bn=
(n∈N*).
设公比为q,则
q+
=
,
解得q=
.
∴bn=
.
(II)∵i,j为正整数,且1≤i≤j≤n,
所有可能的乘积aibj的和=a1
bj+a2
bk+…+an-1
bn-1+anbn
=1×
+2×
+…+(n-1)(
+
)+
.
=1-
+2(
-
)+3(
-
)+…+(n-1)(
-
)+n(
-
)
=(1+
+
+…+
)-
(1+2+…+n),
令Sn=1+
+
+…+
,
Sn=
+
+…+
+
,
∴
Sn=1+
+
+
+…+
-
=1+
+
+
+…+
-
=
-
=2-
.
∴Sn=4-
.
∴所有可能的乘积aibj的和=4-
-
=4-
.
∴n=1时,2a1=
| a | 2 1 |
当n≥2时,2an=2(Sn-Sn-1)=an2+an-(
| a | 2 n-1 |
化为(an+an-1)(an-an-1-1)=0,
∴an-an-1=1.
∴数列{an}是等差数列,
∴an=1+(n-1)×1=n.
∵等比数列{bn}满足b1=
| 1 |
| 2 |
| 3 |
| 2n+1 |
设公比为q,则
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
解得q=
| 1 |
| 2 |
∴bn=
| 1 |
| 2n |
(II)∵i,j为正整数,且1≤i≤j≤n,
所有可能的乘积aibj的和=a1
| n |
 |
| j=1 |
| n |
 |
| k=2 |
| n |
 |
| l=n-1 |
=1×
| ||||
1-
|
| ||||
1-
|
| 1 |
| 2n-1 |
| 1 |
| 2n |
| n |
| 2n |
=1-
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 2n |
| 1 |
| 22 |
| 1 |
| 2n |
| 1 |
| 2n-2 |
| 1 |
| 2n |
| 1 |
| 2n-1 |
| 1 |
| 2n |
=(1+
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2n |
令Sn=1+
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| n-1 |
| 2n-1 |
| n |
| 2n |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| n |
| 2n |
1-
| ||
1-
|
| n |
| 2n |
| n+2 |
| 2n |
∴Sn=4-
| n+2 |
| 2n-1 |
∴所有可能的乘积aibj的和=4-
| n+2 |
| 2n-1 |
| n(n+1) |
| 2n+1 |
| n2+5n+8 |
| 2n+1 |
点评:本题考查了利用“n=1时,a1=S1;n≥2时,an=Sn-Sn-1”求数列的通项公式方法、等差数列与等比数列的通项公式性质、“错位相减法”与等比数列的前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
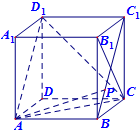 如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列命题:
如图,P是正方体ABCD-A1B1C1D1中BC1上的动点,下列命题:①AP⊥B1C;
②BP与CD1所成的角是60°;
③VP-AD1C为定值;
④B1P∥平面D1AC;
⑤二面角P-AB-C的平面角为45°.
其中正确命题的个数有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
已知各项均为正数的等差数列{an}的前20项和为100,那么a2•a19的最大值是( )
| A、50 | ||
| B、25 | ||
| C、100 | ||
D、4
|
 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,