题目内容
20.在△ABC中,角A、B、C所对的边分别为a,b,c,且a(sinA-sinB)+bsinB=csinC.(Ⅰ)求角c的值
(Ⅱ)若2cos2$\frac{A}{2}$-2sin2$\frac{B}{2}$=$\frac{\sqrt{3}}{2}$,且A<B,求$\frac{c}{a}$的值.
分析 (Ⅰ)根据正弦定理化简已知的式子,由余弦定理求出cosC的值,由内角的范围和特殊角的三角函数值求出角C的值;
(Ⅱ)由二倍角余弦公式的变形化简已知的式子,由(I)和内角和定理求出B的表达式,由A和B大小关系判断A是锐角,代入化简后的式子,由两角差的余弦公式、两角和的正弦公式化简后,由A的范围和特殊角的三角函数值求出A、B,由正弦定理可求出$\frac{c}{a}$的值.
解答 解:(Ⅰ)∵a(sinA-sinB)+bsinB=csinC,
∴由正弦定理得,a(a-b)+b2=c2,
则a2+b2-c2=ab,
∴由余弦定理得,cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{1}{2}$,
∵0<C<π,∴C=$\frac{π}{3}$;
(Ⅱ)∵2cos2$\frac{A}{2}$-2sin2$\frac{B}{2}$=$\frac{\sqrt{3}}{2}$,
∴1+cosA-(1-cosB)=$\frac{\sqrt{3}}{2}$,
则cosA+cosB=$\frac{\sqrt{3}}{2}$,
由C=$\frac{π}{3}$得,A+B=π-C=$\frac{2π}{3}$,
∵A<B,∴A是锐角,且B=$\frac{2π}{3}$-A,
代入上式得,cosA+cos($\frac{2π}{3}$-A)=$\frac{\sqrt{3}}{2}$,
∴cosA$-\frac{1}{2}$cosA+$\frac{\sqrt{3}}{2}$sinA=$\frac{\sqrt{3}}{2}$,
则$\frac{1}{2}$cosA+$\frac{\sqrt{3}}{2}$sinA=$\frac{\sqrt{3}}{2}$,即sin(A+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$,
∵A是锐角,∴A=$\frac{π}{6}$,则B=$\frac{π}{2}$,
由正弦定理得,$\frac{c}{a}$=$\frac{sinC}{sinA}$=$\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=$\sqrt{3}$.
点评 本题考查正弦定理,余弦定理,二倍角余弦公式的变形、两角和的正弦公式等等的应用,注意内角的范围,考查转化思想,化简、变形能力.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案| A. | (-$\frac{2π}{3}$,0) | B. | ($\frac{2π}{3}$,0) | C. | ($\frac{π}{12}$,0) | D. | (-$\frac{π}{6}$,0) |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
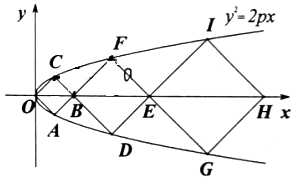 如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )
如图所示,O是坐标原点,三个正方形OABC、BDEF、EGHI的顶点中,O、A、C、D、F、G、I七个点都在抛物线y2=2px(p>0)上,另外,B、E、H三个点都在x轴上,则这三个正方形的面积之比( )| A. | 1:2:3 | B. | 1:4:9 | C. | 2:3:4 | D. | 4:9:16 |
| A. | (-∞,-2) | B. | [-2,0) | C. | (-2,0) | D. | (0,2) |
| A. | {-1,1} | B. | {-1,0,1} | C. | {-1,0,1,2} | D. | {-1,0,1,2,3,5} |