题目内容
若球O的表面积为4π，则球O的体积为 ．
考点：球的体积和表面积
专题：空间位置关系与距离
分析：根据球的表面积与体积公式，求出球的半径即可．
解答：
解：设球O的半径为R，则；
4πR2=4π，
∴R=1；
∴球O的体积为V=
×π×13=
π．
故答案为：
．
4πR2=4π，
∴R=1；
∴球O的体积为V=
| 4 |
| 3 |
| 4 |
| 3 |
故答案为：
| 4π |
| 3 |
点评：本题考查了球的表面积与体积公式的应用问题，是基础题目．
练习册系列答案
相关题目
下列各组函数中，表示同一函数的是（ ）
| A、f（x）=x2，g（x）=1 | |||
B、f（x）=|x|，g（x）=（
| |||
C、f（x）=x，g（x）=
| |||
D、f（x）=x，g（x）=
|
若z=1+i，则
+i
=（ ）
| z |
| i |
. |
| z |
| A、-2 | B、-2i | C、2 | D、2i |
椭圆E：
+
=1以正方形ABCD的顶点A、C为焦点，且过AB、CB的中点M、N，则椭圆E的离心率e等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若椭圆
+y2=1（a＞1）的离心率为
，则该椭圆的长轴长为（ ）
| x2 |
| a2 |
| 1 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
在梯形ABCD中，AB∥CD，如果分别以下列各选项所给的内容作为已知条件，那么其中不能确定BD长度的选项是（ ）| A、AC=4，∠ABD=45°，∠ACD=30° | ||
B、AB=2，CD=2
| ||
C、AB=2，CD=2
| ||
D、CD=2
|
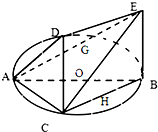如图，一简单几何体的一个面ABC内接于圆O，G、H分别是AE、BC的中点，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．