题目内容
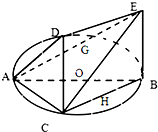 如图,一简单几何体的一个面ABC内接于圆O,G、H分别是AE、BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,一简单几何体的一个面ABC内接于圆O,G、H分别是AE、BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.(1)求证:GH∥平面ACD;
(2)若AB=2,BC=1,tan∠EAB=
| ||
| 2 |
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)连结GO,OH,由已知得GO∥平面ACD,OH∥平面ACD,由此能证明GH∥平面ACD.
(2)由V=VE-ABC+VE-ACD,能求出该几何体的V.
(2)由V=VE-ABC+VE-ACD,能求出该几何体的V.
解答:
(1)证明:连结GO,OH,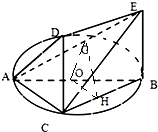
∵GO∥AD,OH∥AC…(2分)
∴GO∥平面ACD,OH∥平面ACD,又GO交HO于O…(4分)
∴平面GOH∥平面ACD…(5分)
∴GH∥平面ACD…(6分)
(2)解:∵V=VE-ABC+VE-ACD…(8分)
∵AB=2,BC=1,tan∠EAB=
,
∴BE=
,AC=
=
.
V=VE-ABC+VE-ACD
=
S△ACB •EB+
S△ACD•DE
=
×
×
×1×
+
×
×
×
×1=1.…(12分)

∵GO∥AD,OH∥AC…(2分)
∴GO∥平面ACD,OH∥平面ACD,又GO交HO于O…(4分)
∴平面GOH∥平面ACD…(5分)
∴GH∥平面ACD…(6分)
(2)解:∵V=VE-ABC+VE-ACD…(8分)
∵AB=2,BC=1,tan∠EAB=
| ||
| 2 |
∴BE=
| 3 |
| AB2-BC2 |
| 3 |
V=VE-ABC+VE-ACD
=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查直线与平面平行的证明,考查几何体的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
执行如图的程序框图,若输出的S=48,则输入k的值可以为( )


| A、4 | B、6 | C、8 | D、10 |
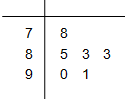 为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )
为了了解某同学的数学学习情况,对他的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,则下列关于该同学数学成绩的说法正确的是( )| A、中位数为83 |
| B、平均数为85 |
| C、众数为85 |
| D、方差为19 |
下列判断正确的是( )
| A、命题“a,b都是偶数,则a+b是偶数”的逆否命题是“若a+b不是偶数,则a,b 都不是偶数 |
| B、若“p或q”为假命题,则“¬p且¬q”是假命题 |
| C、已知a,b,c是实数,关于x的不等式ax2+bx+c≤0的解集是空集,必有a>0且∨≤0 |
| D、x2≠y2?x≠y且x≠-y |
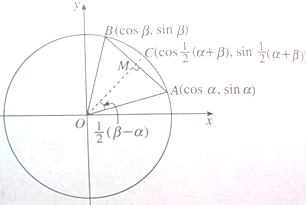 你能利用如图,给出下列两个等式的一个证明吗?
你能利用如图,给出下列两个等式的一个证明吗?