题目内容
已知抛物线C:y=2x2,直线y=kx+2交C于A,B两点,M是线段AB的中点,过M作x轴的垂线交C于点N.
(1)证明:抛物线C在点N处的切线与AB平行;
(2)是否存 在实数k使
在实数k使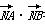 =0,若存在,求k的值;若不存在,说明理由.
=0,若存在,求k的值;若不存在,说明理由.
1)证明

如图,设A(x1,2x ),B(x2,2x
),B(x2,2x
 ),把y=kx+2代入y=2x2得2x2-kx-2=0,
),把y=kx+2代入y=2x2得2x2-kx-2=0,
由韦达定理得x1+x2= ,x1x2=-1,
,x1x2=-1,
 将y=2x2代入上式得2x2-mx+
将y=2x2代入上式得2x2-mx+ -
- =0,
=0,
∵直线l与抛物线C相切,
∴Δ=m2-8∴Δ=m2-8 =m2-2mk+k2
=m2-2mk+k2
=m2-2mk+k2
=(m- k)2=0,∴m=k.
k)2=0,∴m=k.
即l∥AB.
(2)假设存在实数k,使 =0,
=0,
则NA⊥NB,
又∵M是AB的中点,∴MN= AB.
AB.
由(1)知yM= (y1+y2)
(y1+y2)
= (kx1+2+kx2+2)
(kx1+2+kx2+2)
= [k(x1+x2)+4]
[k(x1+x2)+4]
 解得k=±2.使
解得k=±2.使 =0.
=0.

练习册系列答案
相关题目

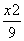 +
+ =1的离心率为
=1的离心率为 ,则k的值为________.
,则k的值为________.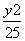 =1共焦点,它们的离心率之和为
=1共焦点,它们的离心率之和为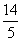 ,求双曲线方程.
,求双曲线方程. +
+ =1内的两定点,点M是椭圆上的动点,求MA+MB的最值.
=1内的两定点,点M是椭圆上的动点,求MA+MB的最值. ,则
,则 的定义域为( )
的定义域为( ) B.
B. C.
C.  D.
D.

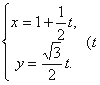 为参数), 曲线
为参数), 曲线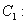
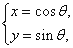 (
(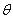 为参数).
为参数). 与
与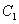 相交于
相交于 两点,求
两点,求 ;
;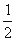 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的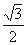 倍,得到曲线
倍,得到曲线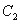 ,设点
,设点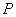 是曲线
是曲线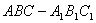 中,侧棱
中,侧棱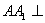 底面
底面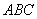 ,
,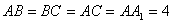 ,点
,点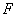 在
在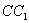 上,且
上,且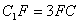 ,
,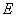 是
是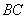 的中点.
的中点.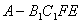 的体积;
的体积; .
.