题目内容
已知A(4,0)，B(2,2)是椭圆
＋
＝1内的两定点，点M是椭圆上的动点，求MA＋MB的最值．
解 因为A(4,0)是椭圆的右焦点，设A′为椭圆的左
焦点，则A′(－4,0)，由椭圆定义知MA＋MA′＝10.
如图所示，则MA＋MB＝MA＋MA′＋MB－MA′＝10＋MB－MA′≤10＋A′B.
当点M在BA′的延长线上时取等号．
所以当M为射线BA′与椭圆的交点时，
(MA＋MB)max＝10＋A′B＝10＋2
.
又如图所示，MA＋MB＝MA＋MA′－MA′＋MB
＝10－(MA′－MB)
≥10－A′B，
当M在A′B的延长线上时取等号．
所以当M为射线A′B与椭圆的交点时，
(MA＋MB)min＝10－A′B＝10－2.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
；
≤
；
2＝9上任意一
点，圆O2以Q(a，b)为圆心且半径为1，当(a－x1)2＋(b－y1)2＝1时，圆O1和圆O2相切．
＋
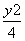＝1有相同的焦点，直线y＝
x为C的一条渐近线．求双曲线C的方程．
线y2＝4x到直线2x－y＋3＝0的距离最小的一点，那么点M的坐标是__________．
在实数k使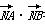
＝0，若存在，求k的值；若不存在，说明理由．
，则
（ ）
）单调递增，则ａ的取值范围是（ ）
B.
C. 
D.
，
．
；
，求函数
的最大值．