题目内容
3.已知线段AB的长为2,动点C满足$\overrightarrow{CA}$•$\overrightarrow{CB}$=λ(λ为负常数),且点C总不在以点B为圆心,$\frac{1}{2}$为半径的圆内,则实数λ的最大值是-$\frac{3}{4}$.分析 由题意建立坐标系,假设点C在圆内,B(0,0),A(2,0),C(rcosa,rsina),(r<$\frac{1}{2}$),从而利用坐标表示出向量,从而可得λ=-2rcosa+r2,从而求得.
解答 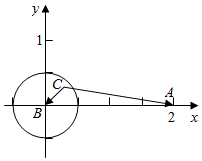 解:由题意建立坐标系如右图,
解:由题意建立坐标系如右图,
假设点C在圆内,
则B(0,0),A(2,0),C(rcosa,rsina),(r<$\frac{1}{2}$),
则$\overrightarrow{CA}$=(2-rcosa,-rsina),$\overrightarrow{CB}$=(-rcosa,-rsina),
∴λ=(2-rcosa,-rsina)•(-rcosa,-rsina)
=-2rcosa+r2(cos2a+sin2a)
=-2rcosa+r2,
∴r2-2r≤λ≤r2+2r,
故-$\frac{3}{4}$<λ<$\frac{5}{4}$,
∵点C总不在以点B为圆心,$\frac{1}{2}$为半径的圆内,
∴λ≤-$\frac{3}{4}$或λ≥$\frac{5}{4}$(舍);
故实数λ的最大值是-$\frac{3}{4}$,
故答案为:-$\frac{3}{4}$.
点评 本题考查了平面向量的坐标表示的应用及数量积的求法,同时考查了数形结合的思想与转化思想的应用.

练习册系列答案
相关题目
12.设直线l:3x+4y+a=0,圆C:(x-2)2+y2=4,若在直线l上存在一点M,使得过M的圆C的切线MP,MQ(P,Q为切点)满足∠PMQ=90°,则a的取值范围是( )
| A. | [-18,6] | B. | [6-5$\sqrt{2}$,6+5$\sqrt{2}$] | C. | [-16,4] | D. | [-6-5$\sqrt{2}$,-6+5$\sqrt{2}$] |
13.已知函数f(x)=-sin$\frac{π}{2}$x-1,g(x)=logax(a>0且a≠1),若F(x)=f(x)-g(x)至少有三个零点,则实数a的取值范围是( )
| A. | (0,$\frac{\sqrt{5}}{5}$) | B. | ($\frac{\sqrt{5}}{5}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |