题目内容
14．在区间[0，1]上随机取两个数x，y，记P为事件“kx≤y≤$\sqrt{x}$”的概率，若P=$\frac{5}{12}$，则实数k=$\frac{1}{2}$．分析 由题意和几何概型以及定积分可得k的方程，解方程可得．
解答 解：在区间[0，1]上随机取两个数x，y，
则总的基本事件构成的区域为{（x，y）|0≤x≤1，0≤y≤1}，为面积为1的正方形，
事件P“kx≤y≤$\sqrt{x}$”的构成的区域为{（x，y）|0≤x≤1，0≤y≤1且kx≤y≤$\sqrt{x}$}，
由定积分可得其面积S=${∫}_{0}^{1}（\sqrt{x}-kx）$dx=（$\frac{2}{3}$${x}^{\frac{3}{2}}$-$\frac{1}{2}$kx2）${|}_{0}^{1}$=$\frac{2}{3}$-$\frac{1}{2}$k，
由P=$\frac{5}{12}$可得$\frac{2}{3}$-$\frac{1}{2}$k=$\frac{5}{12}$，解得k=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 本题考查几何概型，涉及定积分求面积，属基础题．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
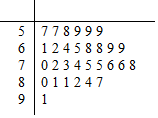2015年7月31日，国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季奥运会（简称冬奥会）在北京和张家口两个城市举办．某中学为了普及奥运会知识，举行了一次奥运知识竞赛．随机抽取了30名学生的成绩，绘成如图所示的茎叶图，若规定成绩在75分以上（包括75分）的学生定义为甲组，成绩在75分以下（不包括75分）定义为乙组．