题目内容
11．甲、乙两位同学玩“套圈”游戏：距离目标2m，轮流对同一目标进行投圈，谁先套住目标谁获胜，已知甲、乙各自套中的概率分别为0.6和0.7，甲先投，求甲恰好套完第三个圈后获胜的概率．分析 问题转化为甲乙两人前2次都没套中且甲第三次套中，由独立事件概率的乘法公式可得．
解答 解：由题意可得甲、乙两位同学投中与否相互独立，
甲恰好套完第三个圈后获胜即甲乙两人前2次都没套中且甲第三次套中，
故所求概率P=（1-0.6）×（1-0.6）×（1-0.7）×（1-0.7）×0.6=0.00864
点评 本题考查相互独立事件的概率的乘法公式，得出甲乙两人前2次都没套中且甲第三次套中是解决问题的关键，属基础题．
练习册系列答案
相关题目
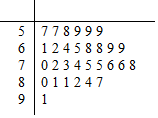2015年7月31日，国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季奥运会（简称冬奥会）在北京和张家口两个城市举办．某中学为了普及奥运会知识，举行了一次奥运知识竞赛．随机抽取了30名学生的成绩，绘成如图所示的茎叶图，若规定成绩在75分以上（包括75分）的学生定义为甲组，成绩在75分以下（不包括75分）定义为乙组．
20．将函数f（x）的图象向左平移φ（0＜φ＜$\frac{π}{2}$）个单位后得到函数g（x）=sin2x的图象，若对满足|f（x1）-g（x2）|=2的x1，x2，有|x1-x2|min=$\frac{π}{3}$，则φ=（ ）
| A． | $\frac{5π}{12}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |
在直三棱柱ABC-A1B1C1中，CA=CB，AA1=$\sqrt{2}$AB，D是AB的中点