题目内容
15.设Sn是数列{an}的前n项和,an>0,且Sn=$\frac{1}{6}$an(an+3)(1)求数列{an}的通项公式;
(2)设cn=$\frac{{a}_{n}}{{2}^{n-1}}$,Bn是数列{cn}的前n项和,求Bn.(若改为cn=an+2n-1呢?)
(3)设bn=$\frac{1}{{(a}_{n}-1)({a}_{n}+2)}$,Tn=b1+b2+…+bn,求证:Tn<$\frac{1}{6}$.
分析 (1)通过Sn=$\frac{1}{6}$an(an+3)与Sn-1=$\frac{1}{6}$an-1(an-1+3)作差、整理可知an-an-1=3,进而可知数列{an}是首项、公差均为3的等差数列,计算即得结论;
(2)①若cn=$\frac{{a}_{n}}{{2}^{n-1}}$,利用错位相减法计算可知Bn=12-6•$\frac{n+2}{{2}^{n}}$;②若cn=an+2n-1,利用分组求和法计算可知Bn=$\frac{3n(n+1)}{2}$+2n-1;
(3)通过(1)裂项可知bn=$\frac{1}{3}$($\frac{1}{3n-1}$-$\frac{1}{3n+2}$),进而并项相加、放缩即得结论.
解答 (1)解:∵Sn=$\frac{1}{6}$an(an+3),
∴当n≥2时,Sn-1=$\frac{1}{6}$an-1(an-1+3),
两式相减得:an=$\frac{1}{6}$an(an+3)-$\frac{1}{6}$an-1(an-1+3),
整理得:(an+an-1)(an-an-1)=3(an+an-1)
又∵an>0,
∴an-an-1=3,
∵S1=$\frac{1}{6}$a1(a1+3),解得:a1=3或a1=0(舍),
∴数列{an}是首项、公差均为3的等差数列,
∴an=3n;
(2)解:①由(1)可知cn=$\frac{{a}_{n}}{{2}^{n-1}}$=3n•$\frac{1}{{2}^{n-1}}$,
∴Bn=3(1•$\frac{1}{{2}^{1-1}}$+2•$\frac{1}{2}$+3•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n-1}}$),
$\frac{1}{2}$Bn=3[1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+(n-1)•$\frac{1}{{2}^{n-1}}$+n•$\frac{1}{{2}^{n}}$],
两式相减得:$\frac{1}{2}$Bn=3(1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$)
=3•($\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n}}$)
=6-3•$\frac{n+2}{{2}^{n}}$,
∴Bn=12-6•$\frac{n+2}{{2}^{n}}$;
②由(1)可知cn=an+2n-1=3n+2n-1,
∴Bn=3•$\frac{n(n+1)}{2}$+$\frac{1-{2}^{n}}{1-2}$=$\frac{3n(n+1)}{2}$+2n-1;
(3)证明:由(1)可知bn=$\frac{1}{{(a}_{n}-1)({a}_{n}+2)}$=$\frac{1}{(3n-1)(3n+2)}$=$\frac{1}{3}$($\frac{1}{3n-1}$-$\frac{1}{3n+2}$),
∴Tn=b1+b2+…+bn
=$\frac{1}{3}$($\frac{1}{3-1}$-$\frac{1}{3+2}$+$\frac{1}{3+2}$-$\frac{1}{3×2+2}$+…+$\frac{1}{3n-1}$-$\frac{1}{3n+2}$)
=$\frac{1}{3}$($\frac{1}{2}$-$\frac{1}{3n+2}$)
<$\frac{1}{6}$.
点评 本题考查数列的通项公式及前n项和,考查错位相减法,考查裂项相消法,考查分组求和法,注意解题方法的积累,属于中档题.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
| A. | {x|x>0} | B. | {x|0<x<1} | C. | {x|x<1} | D. | {x|x≤0} |
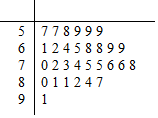 2015年7月31日,国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季奥运会(简称冬奥会)在北京和张家口两个城市举办.某中学为了普及奥运会知识,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.
2015年7月31日,国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季奥运会(简称冬奥会)在北京和张家口两个城市举办.某中学为了普及奥运会知识,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.