题目内容
已知函数f(x)=ax-lnx+1(a∈R),g(x)=xe1-x.
(1)求函数g(x)在区间(0,e]上的值域;
(2)是否存在实数a,对任意给定的x0∈(0,e],在区间[1,e]上都存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立.若存在,求出a的取值范围;若不存在,请说明理由.
(1)求函数g(x)在区间(0,e]上的值域;
(2)是否存在实数a,对任意给定的x0∈(0,e],在区间[1,e]上都存在两个不同的xi(i=1,2),使得f(xi)=g(x0)成立.若存在,求出a的取值范围;若不存在,请说明理由.
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)由g′(x)=e1-x-xe1-x=e1-x(1-x),知g(x)在区间(0,1]上单调递增,在区间[1,e)上单调递减,由此能求出g(x)的值域.
(2)设m=g(x),则由(1)可得m∈(0,1],原问题等价于:对任意的t∈(0,1],f(x)=m在[1,e]上总有两个不同的实根,故f(x)在[1,e]不可能是单调函数,由此能推导出满足条件的a不存在.
(2)设m=g(x),则由(1)可得m∈(0,1],原问题等价于:对任意的t∈(0,1],f(x)=m在[1,e]上总有两个不同的实根,故f(x)在[1,e]不可能是单调函数,由此能推导出满足条件的a不存在.
解答:
解:(1)∵g′(x)=e1-x-xe1-x=e1-x(1-x),
∴g(x)在区间(0,1]上单调递增,在区间[1,e)上单调递减,
且g(0)=0,g(1)=1>g(e)=e2-e,
∴g(x)的值域为(0,1].
(2)设m=g(x),则由(1)可得m∈(0,1],
原问题等价于:对任意的m∈(0,1],f(x)=m在[1,e]上总有两个不同的实根,
故f(x)在[1,e]不可能是单调函数,
∵f′(x)=a-
,(1≤x≤e),其中
∈[
,1],
①当a≥1时,f′(x)>0,f(x)在区间[1,e]上单调递增,不合题意.
②当a≤
时,f′(x)<0,f(x)在区间[1,e]上单调递减,不合题意.
③当1<
<e,即
<a<1时,f(x)在区间[1,
]上单调递减;f(x)在区间[
,e]上单递增,
由上可得a∈(
,1),此时必有f(x)的最小值小于等于0,且f(x)的最大值大于等于1,
而由f(x)min=f(
)=2+lna≤0,可得a≤
<
,则a∈∅.
综上,满足条件的a不存在.
∴g(x)在区间(0,1]上单调递增,在区间[1,e)上单调递减,
且g(0)=0,g(1)=1>g(e)=e2-e,
∴g(x)的值域为(0,1].
(2)设m=g(x),则由(1)可得m∈(0,1],
原问题等价于:对任意的m∈(0,1],f(x)=m在[1,e]上总有两个不同的实根,
故f(x)在[1,e]不可能是单调函数,
∵f′(x)=a-
| 1 |
| x |
| 1 |
| x |
| 1 |
| e |
①当a≥1时,f′(x)>0,f(x)在区间[1,e]上单调递增,不合题意.
②当a≤
| 1 |
| e |
③当1<
| 1 |
| a |
| 1 |
| e |
| 1 |
| a |
| 1 |
| a |
由上可得a∈(
| 1 |
| e |
而由f(x)min=f(
| 1 |
| a |
| 1 |
| e2 |
| 1 |
| e |
综上,满足条件的a不存在.
点评:本题考查函数的值域的求法,探索是否存在满足条件的实数,探索函数图象上满足条件的两点是否存在.综合性强,难度大,对数学思维能力要求较高,有一定的探索性.

练习册系列答案
相关题目
定义运算a*b=
,例如1*2=1,则2*a的取值范围是( )
|
| A、(0,2) |
| B、(-∞,2] |
| C、[0,2] |
| D、[2,+∞) |
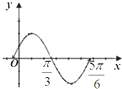
已知函数y=2sin(ωx+φ)(ω>0,|φ|<
)的图象的一部分如图所示,则( )
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=-
| ||
C、ω=2,φ=
| ||
D、ω=2,φ=-
|