题目内容
已知θ是直线y=2x的倾斜角,则cosθ=( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
考点:直线的倾斜角
专题:直线与圆
分析:利用直线的倾斜角和直线的斜率求解.
解答:
解:∵θ是直线y=2x的倾斜角,
∴tanθ=2,
∴
=
=2,
解得cosθ=
,或cosθ=-
(舍)
∴cosθ=
.
故选:B.
∴tanθ=2,
∴
| sinθ |
| cosθ |
| ||
| cosθ |
解得cosθ=
| ||
| 5 |
| ||
| 5 |
∴cosθ=
| ||
| 5 |
故选:B.
点评:本题考查直线的倾斜角的余弦值的求法,是基础题,解题时要注意直线的斜率的灵活运用.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
某程序框图如图所示,该程序运行后输出S的值是( )


| A、8 | B、10 | C、31 | D、63 |
已知圆柱的底面半径为2,高为3,用一个与底面不平行的平面去截,若所截得的截面为椭圆,则椭圆的离心率的最大值为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
函数f(x)=ln(x+1)-
+1的零点所在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
一个正三棱柱的三视图如图所示,则这个正三棱柱的高和底面边长分别为( )


A、1,
| ||
B、
| ||
| C、2,1 | ||
| D、1,2 |
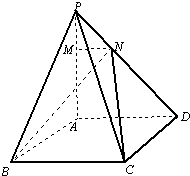 已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=120°,PA=AB=2
已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=120°,PA=AB=2