题目内容
1.设A,B为抛物线y2=2px(p>0)上相异两点,则${|{\overrightarrow{OA}+\overrightarrow{OB}}|^2}-{|{\overrightarrow{AB}}|^2}$的最小值为-4p2.分析 设A(xA,yA),B(xB,yB).则${|{\overrightarrow{OA}+\overrightarrow{OB}}|^2}-{|{\overrightarrow{AB}}|^2}$=4(xA•xB+yA•yB),分类讨论,结合韦达定理,${|{\overrightarrow{OA}+\overrightarrow{OB}}|^2}-{|{\overrightarrow{AB}}|^2}$=4(a2-2ap)=4[(a-p)2-p2]≥-4p2即可得出结论.
解答 解:设A(xA,yA),B(xB,yB).则$\overrightarrow{OA}$+$\overrightarrow{OB}$=(xA+xB,yA+yB),$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=(xB-xA,yB-yA),
${|{\overrightarrow{OA}+\overrightarrow{OB}}|^2}-{|{\overrightarrow{AB}}|^2}$=4(xA•xB+yA•yB),
若直线AB斜率存在,设为y=k(x-a),
则$\left\{\begin{array}{l}{y=k(x-a)}\\{{y}^{2}=2px}\end{array}\right.$,整理得:k2x2-2(ak2+p)x+k2a2=0,
xA•xB=a2,yA•yB=k2(xA-a)(xB-a)=-2ap,
${|{\overrightarrow{OA}+\overrightarrow{OB}}|^2}-{|{\overrightarrow{AB}}|^2}$=4(xA•xB+yA•yB)=4(a2-2ap)=4[(a-p)2-p2]≥-4p2,.
若直线不存在,当xA=xB=a,yA=-yB=$\sqrt{2ap}$时,上式也成立.
故所求最小值为-4p2.
当且仅当直线AB过点(p,0)时等号成立,
故答案为:-4p2.
点评 本题考查了抛物线的简单几何性质,考查了学生的计算能力,体现了分类讨论的数学思想方法,是中档题.

| A. | 命题“若x2-4x+3=0,则x=3或x=1”的逆否命题是“若x≠3且x≠1,则x2-4x+3=0≠0” | |
| B. | “x2-x=0”是“x=1”的必要不充分条件 | |
| C. | 若p∨q为真命题,则p,q均为真命题 | |
| D. | 命题p:?x∈R,使得x3+x+1=0,则¬p:?x∈R,使得x3+x+1≠0 |
| A. | 至少有1件次品与至多有1件正品 | B. | 恰有1件次品与恰有2件正品 | ||
| C. | 至少有1件次品与至少有1件正品 | D. | 至少有1件次品与都是正品 |
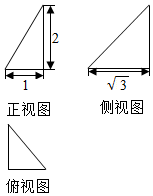 某几何体的三视图如图所示,则该几何体外接球的表面积为( )
某几何体的三视图如图所示,则该几何体外接球的表面积为( )| A. | $\frac{25π}{4}$ | B. | $\frac{25π}{8}$ | C. | 12π | D. | 8π |
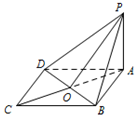
| A. | PD⊥CD | B. | BD⊥平面PAO | C. | PB⊥CB | D. | BC∥平面PAD |
 函数y=2sinπx(x∈R)的部分图象如图所示,设O为坐标原点,P是图象的最高点,B是图象与x轴的交点,则tan∠OPB的值为$\frac{16}{3}$.
函数y=2sinπx(x∈R)的部分图象如图所示,设O为坐标原点,P是图象的最高点,B是图象与x轴的交点,则tan∠OPB的值为$\frac{16}{3}$.