题目内容
若1<a<b,求证0<
<1.
| (b+1)(a-1) |
| (b-1)(a+1) |
考点:不等式的证明
专题:证明题,综合法
分析:根据1<a<b,可得b+1>a+1>0,b-1>a-1>0,从而
>0,证明
-1<0,即可得出结论.
| (b+1)(a-1) |
| (b-1)(a+1) |
| (b+1)(a-1) |
| (b-1)(a+1) |
解答:
证明:∵1<a<b,
∴b+1>a+1>0,b-1>a-1>0,
∴
>0,
∵
-1=
<0,
∴
<1,
∴0<
<1.
∴b+1>a+1>0,b-1>a-1>0,
∴
| (b+1)(a-1) |
| (b-1)(a+1) |
∵
| (b+1)(a-1) |
| (b-1)(a+1) |
| 2(a-b) |
| (b-1)(a+1) |
∴
| (b+1)(a-1) |
| (b-1)(a+1) |
∴0<
| (b+1)(a-1) |
| (b-1)(a+1) |
点评:本题考查不等式的证明,考查作差法的运用,属于中档题.

练习册系列答案
相关题目
在ABC中,a,b,c分别为角A,B,C的对边,且角A=60°,若S△ABC=
,且5sinB=3sinC,则ABC的周长等于( )
15
| ||
| 4 |
A、8+
| ||
| B、14 | ||
C、10+3
| ||
| D、18 |
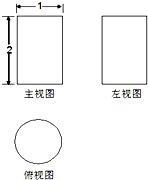 一个空间几何体的主视图和左视图都是矩形,俯视图是一个的圆,尺寸如图,那么这个几何体的侧面积为
一个空间几何体的主视图和左视图都是矩形,俯视图是一个的圆,尺寸如图,那么这个几何体的侧面积为