题目内容
11.二次曲线$\left\{{\begin{array}{l}{x=5cosθ}\\{y=3sinθ}\end{array}}\right.$(θ是参数)的左焦点的坐标是(-4,0).分析 消去参数θ可得普通方程,易得左焦点坐标.
解答 解:∵二次曲线$\left\{{\begin{array}{l}{x=5cosθ}\\{y=3sinθ}\end{array}}\right.$(θ是参数),
∴cosθ=$\frac{x}{5}$,sinθ=$\frac{y}{3}$,
由cos2θ+sin2θ=1可得$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,
∴a=5,b=3,c=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴该椭圆的左焦点为(-4,0)
故答案为:(-4,0)
点评 本题考查椭圆的参数方程,消参数化为普通方程是解决问题的关键,属基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
19.双曲线4x2-y2=1的一条渐近线的方程为( )
| A. | 2x+y=0 | B. | 2x+y=1 | C. | x+2y=0 | D. | x+2y=1 |
20.若双曲线C:x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的顶点到渐近线的距离为$\frac{\sqrt{2}}{2}$,则双曲线的离心率e=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{3}$ |
1.过原点的直线l与双曲线$\frac{x^2}{9}-\frac{y^2}{3}=-1$有两个交点,则直线l的斜率的取值范围是( )
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $({-∞,-\frac{{\sqrt{3}}}{3}})∪({\frac{{\sqrt{3}}}{3},+∞})$ | C. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | D. | $({-∞,-\frac{{\sqrt{3}}}{3}]∪[\frac{{\sqrt{3}}}{3},+∞})$ |

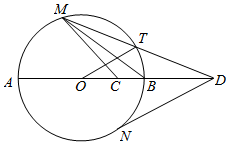 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT