题目内容
11.在△ABC中,已知$\frac{sin(A-B)}{sin(A+B)}$=$\frac{2c-b}{2c}$,求sin$\frac{A}{2}$的值.分析 由三角形的知识以及和差角的三角函数公式化简可得cosA,再由二倍角公式可得.
解答 解:∵在△ABC中$\frac{sin(A-B)}{sin(A+B)}$=$\frac{2c-b}{2c}$,
∴$\frac{sin(A-B)}{sinC}$=$\frac{2sinC-sinB}{2sinC}$,
∴2sin(A-B)=2sinC-sinB=2sin(A+B)-sinB,
∴2sinAcosB-2cosAsinB=2sinAcosB+2cosAsinB-sinB,
∴4cosAsinB=sinB,故cosA=$\frac{1}{4}$,即1-2sin2$\frac{A}{2}$=$\frac{1}{4}$,
解得sin$\frac{A}{2}$=$\frac{\sqrt{6}}{4}$,或-$\frac{\sqrt{6}}{4}$(舍去负值)
点评 本题考查两角和与差的三角函数公式以及三角形的知识,属中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
2.已知多项式x2+x10=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,则a2=( )
| A. | 32 | B. | 42 | C. | 46 | D. | 56 |
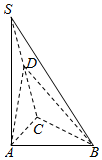 如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,点D是SC的中点,且平面ABD⊥平面SAC.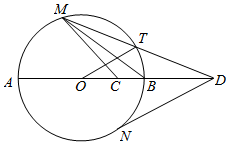 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT