题目内容
12.根据下列条件求方程.(1)若抛物线y2=2px的焦点与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的右焦点重合,求抛物线的准线方程(5分)
(2)已知双曲线的离心率等于2,且与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1有相同的焦点,求此双曲线标准方程.(5分)
分析 (1)求得椭圆的右焦点,抛物线的焦点,由题意可得p=4,进而得到抛物线的准线方程;
(2)求出椭圆的焦点,设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),由题意可得c=4,运用a,b,c的关系和离心率公式,解方程可得a,b,进而得到双曲线的标准方程.
解答 解:(1)易知椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的右焦点为(2,0),
由抛物线y2=2px的焦点($\frac{p}{2}$,0)与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的右焦点重合,
可得p=4,
可得抛物线y2=8x的准线方程为x=-2.
(2)椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的焦点为(-4,0)和(4,0),
可设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),
由题意可得c=4,即a2+b2=16,
又e=$\frac{c}{a}$=2,
解得a=2,b=2$\sqrt{3}$,
则双曲线的标准方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1.
点评 本题考查圆锥曲线的方程和性质,主要是抛物线的准线方程和双曲线的方程的求法,注意运用待定系数法,考查运算能力,属于基础题.

练习册系列答案
相关题目
20.若双曲线C:x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的顶点到渐近线的距离为$\frac{\sqrt{2}}{2}$,则双曲线的离心率e=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{3}$ |
7.已知双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$的左右焦点分别为F1,F2,O为坐标原点,P为双曲线右支上一点,△F1PF2的内切圆的圆心为Q,过F2作PQ的垂线,垂足为B,则OB的长度为( )
| A. | $\sqrt{7}$ | B. | 4 | C. | 3 | D. | 2 |
1.过原点的直线l与双曲线$\frac{x^2}{9}-\frac{y^2}{3}=-1$有两个交点,则直线l的斜率的取值范围是( )
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $({-∞,-\frac{{\sqrt{3}}}{3}})∪({\frac{{\sqrt{3}}}{3},+∞})$ | C. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | D. | $({-∞,-\frac{{\sqrt{3}}}{3}]∪[\frac{{\sqrt{3}}}{3},+∞})$ |
2.已知双曲线$\frac{{x}^{2}}{k}+\frac{{y}^{2}}{6+k}=1$的实轴长为4,则双曲线的渐近线方程为( )
| A. | y=$±\frac{1}{2}x$ | B. | y=±x | C. | y=±2x | D. | y=±$\sqrt{2}x$ |
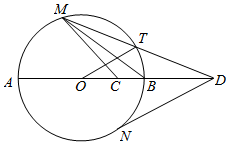 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT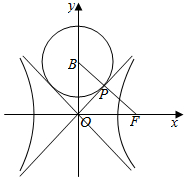 如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.
如图,双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)虚轴上的端点B(0,b),右焦点F,若以B为圆心的圆与C的一条渐近线相切于点P,且$\overrightarrow{BP}$∥$\overrightarrow{PF}$,则该双曲线的离心率为$\frac{1+\sqrt{5}}{2}$.