题目内容
已知正项数列{an}的前n项和为Sn,且Sn=(
)2+
.
(1)求数列{an}的通项公式;
(2)若Tn=
+
+
+…+
,求证:Tn<
+1.
| an |
| 2 |
| an |
| 2 |
(1)求数列{an}的通项公式;
(2)若Tn=
| a12+1 |
| a12-1 |
| a22+1 |
| a22-1 |
| a32+1 |
| a32-1 |
| an2+1 |
| an2-1 |
| an |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由Sn=(
)2+
,得4Sn=an2+2an,由此推导出an+1-an-2=0,从而能求出an=2n,n∈N*.
(2)由
=
=1+
=1+
-
,利用分组求和法和裂项求和法能证明Tn<
+1.
| an |
| 2 |
| an |
| 2 |
(2)由
| an2+1 |
| an2-1 |
| 4n2+1 |
| 4n2-1 |
| 2 |
| 4n2-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| an |
| 2 |
解答:
解:(1)∵Sn=(
)2+
,
∴4Sn=an2+2an,4Sn+1=an+12+2an+1
4Sn+1-4Sn=4an+1=an+12-an2+2an+1-2an
(an+1+an)(an+1-an)-2(an+1+an)=0
(an+1+an)(an+1-an-2)=0
∵{an}是正项数列,∴an+1-an-2=0,
又∵a1=S1=
+
,解得a1=2,或a1=0,(舍).
∴数列{an}是首项为2、公差为2的等差数列,
∴an=2n,n∈N*.
(2)∵
=
=1+
=1+
-
,
∴Tn=n+(1-
+
-
+…+
-
)
=n+1-
<n+1
=
+1.
∴Tn<
+1.
| an |
| 2 |
| an |
| 2 |
∴4Sn=an2+2an,4Sn+1=an+12+2an+1
4Sn+1-4Sn=4an+1=an+12-an2+2an+1-2an
(an+1+an)(an+1-an)-2(an+1+an)=0
(an+1+an)(an+1-an-2)=0
∵{an}是正项数列,∴an+1-an-2=0,
又∵a1=S1=
| a12 |
| 4 |
| a1 |
| 2 |
∴数列{an}是首项为2、公差为2的等差数列,
∴an=2n,n∈N*.
(2)∵
| an2+1 |
| an2-1 |
| 4n2+1 |
| 4n2-1 |
| 2 |
| 4n2-1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=n+(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=n+1-
| 1 |
| 2n+1 |
<n+1
=
| an |
| 2 |
∴Tn<
| an |
| 2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法和分组求和法的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知向量
=(1,k),
=(2,k-3),且
∥
,则k的值为( )
| a |
| b |
| a |
| b |
| A、-3 | B、0 | C、1 | D、3 |
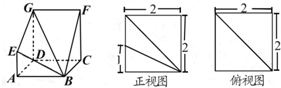 如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图:
如图,多面体ABCD-EFG中,底面ABCD为正方形,GD∥FC∥AE,AE⊥平面ABCD,其正视图、俯视图及相关数据如图: