题目内容
已知PA⊥正方形ABCD所在的平面，垂足为A，连结PB，PC，PD，AC，BD，则互相垂直的平面有（ ）
| A、5对 | B、6对 | C、7对 | D、8对 |
考点：平面与平面之间的位置关系
专题：空间位置关系与距离
分析：由已知条件推导出互相垂直的平面有：平面PAB⊥平面ABCD；平面PAD⊥平面ABCD；平面PAC⊥平面ABCD；平面PAB⊥平面PAD；平面PCD⊥平面PAD；平面PBC⊥平面PAB；平面PBD⊥平面PAC．
解答：
解：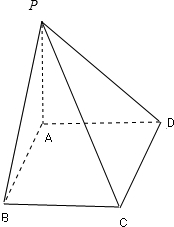
如图，∵PA⊥正方形ABCD所在的平面，垂足为A，
∴PA⊥平面ABCD，
∵PA?平面PAB，∴平面PAB⊥平面ABCD；
∵PA?平面PAD，∴平面PAD⊥平面ABCD；
∵PA?平面PAC，∴平面PAC⊥平面ABCD；
∵PA⊥AB，AD⊥AB，∴AB⊥平面PAD，
∵AB?平面PAB，∴平面PAB⊥平面PAD；
同理，CD⊥平面PAD，
∵CD?平面PCD，∴平面PCD⊥平面PAD；
同理，BC⊥平面PAB，
∵BC?平面PBC，∴平面PBC⊥平面PAB；
∵AC⊥BD，PA⊥BD，∴BD⊥平面PAC，
∵BD?平面PBD，∴平面PBD⊥平面PAC．
故选：C．
如图，∵PA⊥正方形ABCD所在的平面，垂足为A，∴PA⊥平面ABCD，
∵PA?平面PAB，∴平面PAB⊥平面ABCD；
∵PA?平面PAD，∴平面PAD⊥平面ABCD；
∵PA?平面PAC，∴平面PAC⊥平面ABCD；
∵PA⊥AB，AD⊥AB，∴AB⊥平面PAD，
∵AB?平面PAB，∴平面PAB⊥平面PAD；
同理，CD⊥平面PAD，
∵CD?平面PCD，∴平面PCD⊥平面PAD；
同理，BC⊥平面PAB，
∵BC?平面PBC，∴平面PBC⊥平面PAB；
∵AC⊥BD，PA⊥BD，∴BD⊥平面PAC，
∵BD?平面PBD，∴平面PBD⊥平面PAC．
故选：C．
点评：本题考查互相垂直的平面对数的判断，是基础题，解题时要注意空间思维能力的培养．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目