��Ŀ����
�躯��f(x)��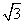 sinxcosx��cos2x��a.
sinxcosx��cos2x��a.
(1)д������f(x)����С�����ڼ������ݼ����䣻
(2)��x��[��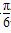 ��
��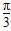 ]ʱ������f(x)�����ֵ����Сֵ�ĺ�Ϊ
]ʱ������f(x)�����ֵ����Сֵ�ĺ�Ϊ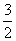 ����f(x)�Ľ���ʽ��
����f(x)�Ľ���ʽ��
(3)������(2)�ĺ���f(x)��ͼ������ƽ��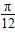 ����λ�������겻�䣬�������Ϊԭ����2����������ƽ��
����λ�������겻�䣬�������Ϊԭ����2����������ƽ�� ����λ���õ�����g(x)��ͼ����g(x)��ͼ����x��������ᡢֱ��x��
����λ���õ�����g(x)��ͼ����g(x)��ͼ����x��������ᡢֱ��x��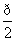 ��Χ��ͼ�ε������
��Χ��ͼ�ε������
(1)f(x)��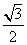 sin2x��
sin2x�� ��a
��a
��sin(2x��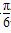 )��a��
)��a�� ��
��
����������T����.
��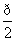 ��2k��2x��
��2k��2x��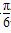 ��
�� ��2k��k��Z��
��2k��k��Z��
��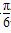 ��k��x��
��k��x�� ��k��k��Z.
��k��k��Z.
�ʺ���f(x)�ĵ����ݼ�������[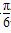 ��k�У�
��k�� ��k��](k��Z)��
��k��](k��Z)��
(2)�ߣ�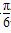 ��x��
��x��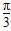 ��
��
�࣭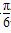 ��2x��
��2x��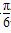 ��
�� .
.
�࣭ ��sin(2x��
��sin(2x��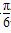 )��1.
)��1.
��x��[��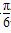 ��
��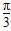 ]ʱ������f(x)�����ֵ��Сֵ�ĺ�(1��a��
]ʱ������f(x)�����ֵ��Сֵ�ĺ�(1��a�� )��(��
)��(�� ��a��
��a�� )��
)��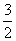 ��
��
��a��0����f(x)��sin(2x��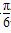 )��
)�� .
.


��ϰ��ϵ�д�
�����Ŀ
 ����f(��4)��2��f(��2)����2�������x�ķ���f(x)��x�Ľ�ĸ�����________��
����f(��4)��2��f(��2)����2�������x�ķ���f(x)��x�Ľ�ĸ�����________��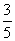 ��cos����
��cos����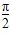 )������������________.
)������������________.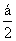 ��3����cos����(����)
��3����cos����(����) B����
B���� D����
D���� ��b��
��b�� ��B��60�㣬��ô��A����(����)
��B��60�㣬��ô��A����(����) D��5
D��5 ��18�����c�ij���
��18�����c�ij��� ��P��BN�ϵ�һ�㣬��
��P��BN�ϵ�һ�㣬�� ����ʵ��m��ֵΪ(����)
����ʵ��m��ֵΪ(����) ��������B.
��������B. ��������C��1��������D��3
��������C��1��������D��3