在${^n}$的二项展开式中.若第四项的系数为-7.则n=( )A．9B．8C．7D．6 题目和参考答案——青夏教育精英家教网——

题目内容

18．在${（\sqrt{x}-{2^{-1}}x）^n}$的二项展开式中，若第四项的系数为-7，则n=（　　）

A．

9

B．

8

C．

7

D．

6

分析先写出其通项，再令r=3，根据第四项的系数为-7，即可求出n的值．

解答解：${（\sqrt{x}-{2^{-1}}x）^n}$的二项展开式的通项为T_r+1=C_n^r（-2^-1）^r${x}^{\frac{n+r}{2}}$，
∵第四项的系数为-7，
∴r=3，
∴C_n³（-2^-1）³=-7，
解得n=8，
故选：B．

点评本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于中档题．

练习册系列答案

QQ教辅中考题库系列答案

小考必备小升初三年真题测试卷系列答案

宏翔文化全国名校中考模拟试题系列答案

三点一测学霸必刷题系列答案

名榜文化假期作业寒假郑州大学出版社系列答案

赢在假期电子科技大学出版社系列答案

金牌教辅中考学霸123系列答案

复习计划风向标寒系列答案

中考命题大解密阳光出版社系列答案

夺冠百分百高效复习系列答案

相关题目

8．已知函数f（x）=x²+（a+2）x+b，若f（-1）=-2，且对于任意实数x都有f（x）≥2x．
（1）求f（x）的解析式；
（2）讨论函数f（x）在区间[-3，1]上的单调性；
（3）求函数f（x）在区间[-3，1]上的值域．

9．已知椭圆x²+$\frac{{y}^{2}}{{b}^{2}}$=1（0＜b＜1），其左、右焦点分别为F₁、F₂，|F₁F₂|=2c．若此椭圆上存在点P，使P到直线x=$\frac{1}{c}$的距离是|PF₁|与|PF₂|的等差中项，则b的最大值为$\frac{\sqrt{3}}{2}$．

6．设数列{a_n}的前n项和为S_n，若${S_n}=1-\frac{2}{3}{a_n}$（n∈N^*），则$\lim_{n→∞}{S_n}$=1．

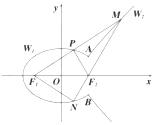如图：椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）有相同的焦点F₁、F₂，它们在y轴右侧有两个交点A、B，满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0．将直线AB左侧的椭圆部分（含A，B两点）记为曲线W₁，直线AB右侧的双曲线部分（不含A，B两点）记为曲线W₂．以F₁为端点作一条射线，分别交W₁于点P（x_P，y_P），交W₂于点M（x_M，y_M）（点M在第一象限），设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$．
（1）求W₂的方程；
（2）证明：x_P=$\frac{1}{m}$，并探索直线MF₂与PF₂斜率之间的关系；
（3）设直线MF₂交W₁于点N，求△MF₁N的面积S的取值范围．

3．已知等差数列{a_n}中，a₁=11，a₅=-1，则{a_n}的前n项和S_n的最大值是（　　）

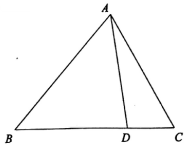在△ABC中，D为BC边上一点，AD=BD，AC=4，BC=5．
（1）若∠C=60°，求△ABC外接圆半径R的值；
（2）设∠CAB-∠B=θ，若$tanθ=\frac{{\sqrt{15}}}{7}$，求△ABC的面积．

7．已知复数z的实部和虚部相等，且z（2+i）=3-bi（b∈R），则|z|=（　　）

8．已知（ax+1）⁵的展开式中各项系数和为243，则二项式${（{\frac{3x}{a}-\frac{1}{{\root{3}{x}}}}）^5}$的展开式中含x项的系数为-$\frac{45}{2}$．（用数字作答）