题目内容
7．
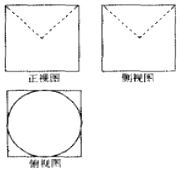某几何体的三视图如图所示，图中四边形都是边长为2的正方形，两条虚线相互垂直，则该几何体的表面积是（ ）| A． | $24+（{\sqrt{2}+1}）π$ | B． | $24+（{\sqrt{2}-1}）π$ | C． | $24-（{\sqrt{2}+1}）π$ | D． | $24-（{\sqrt{2}-1}）π$ |
分析 由三视图知原几何体是一个棱长为2的正方体挖去一圆锥得到的，根据所提供的数据可求出正方体、圆锥的表面积．
解答 解：由三视图知原几何体是一个棱长为2的正方体挖去一圆锥得到的，
该圆锥的底为正方形的内切圆，高为1，
∴该几何体的体积为6×22-π+π×1×$\sqrt{2}$=24+（$\sqrt{2}-1$）π．
故选B．
点评 本题主要考查三视图的应用，以及空间几何体的表面积计算，要求熟练掌握常见几何体的表面积公式．
练习册系列答案
相关题目
18．在区间[-1，4]上随机选取一个数x，则x≤1的概率为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{1}{5}$ | D． | $\frac{2}{3}$ |
2．已知点p（x，y）满足$\left\{\begin{array}{l}x+y-2\sqrt{2}≥0\\ x≤2\sqrt{2}\\ y≤2\sqrt{2}\end{array}\right.$过点p（x，y）向圆x2+y2=1做两条切线，切点分别是点A和点B，则当∠APB最大时，$\overrightarrow{PA}•\overrightarrow{PB}$的值是（ ）
| A． | 2 | B． | 3 | C． | $\frac{5}{2}$ | D． | $\frac{3}{2}$ |
19．设f'（x）是函数f（x）定义在（0，+∞）上的导函数，满足$xf'（x）+2f（x）=\frac{1}{x^2}$，则下列不等式一定成立的是（ ）
| A． | $\frac{f（e）}{e^2}＞\frac{{f（{e^2}）}}{e}$ | B． | $\frac{f（2）}{9}＜\frac{f（3）}{4}$ | C． | $\frac{f（2）}{e^2}＞\frac{f（e）}{4}$ | D． | $\frac{f（e）}{e^2}＜\frac{f（3）}{9}$ |
9．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}-2x+1（x≤0）}\\{|lo{g}_{2}x|（x＞0）}\end{array}\right.$，若方程f（x）=k有四个不同的实数根，x1、x2、x3、x4，则x1+x2+x3+x4的取值范围是（ ）
| A． | [0，$\frac{1}{2}$] | B． | [$\frac{1}{2}$，$\frac{9}{4}$） | C． | [$\frac{1}{2}$，$\frac{9}{4}$] | D． | [$\frac{9}{4}$，+∞） |