题目内容
利用定义判断函数f（x）=x+
在区间（-∞，+∞）上的单调性．
| x2+1 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：可设x1＜x2，已知函数的解析式，利用定义法进行求解；
解答：
解：∵f（x）=x+
在区间（-∞，+∞）上，可以设x1＜x2
可得f（x1）-f（x2）=x1+
-（x2+
）=（x1-x2）+（
-
）=（x1-x2）-
=（x1-x2）（1+
），
∵1+
＞1+
＞1+1=2，
又∵x1＜x2，x1-x2＜0，
∴（x1-x2）（1+
）＜0，
∴f（x1）＜f（x2），
∴f（x）在区间（-∞，+∞）上为增函数，
同故函数f（x）=x+
在区间（-∞，+∞）上为增函数
| x2+1 |
可得f（x1）-f（x2）=x1+
| x12+1 |
| x22+1 |
| x12+1 |
| x22+1 |
| (x2-x1)(x2+x1) | ||||
|
| x2+x1 | ||||
|
∵1+
| x2+x1 | ||||
|
| x2+x1 | ||||
|
又∵x1＜x2，x1-x2＜0，
∴（x1-x2）（1+
| x2+x1 | ||||
|
∴f（x1）＜f（x2），
∴f（x）在区间（-∞，+∞）上为增函数，
同故函数f（x）=x+
| x2+1 |
点评：本题主要考查函数的单调性的判断与证明，是一道基础题，考查的知识点比较单一；
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
双曲线
-y2=-1的离心率为（ ）
| x2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知m，n为不同的直线，α，β为不同的平面，则下列说法正确的是（ ）
| A、m?α，n∥m⇒n∥α |
| B、m?α，n⊥m⇒n⊥α |
| C、m?α，n?β，m∥n⇒α∥β |
| D、n?β，n⊥α⇒α⊥β |
已知条件p：x＞1或x＜-3，条件q：x＞a，且q是p的充分而不必要条件，则a的取值范围是（ ）
| A、a≥1 | B、a≤1 |
| C、a≥-3 | D、a≤-3 |
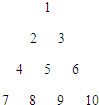把正整数按上小下大、左小右大的原则排成如图三角形数表（每行比上一行多一个数）：设ai，j（i、j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a4，2=8，则a51，25为