题目内容
设(x-
)6的展开式中x3的系数为a,二项式系数为b,则
的值为 .
| 2 | ||
|
| a |
| b |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于3,求出r的值,即可求得展开式中x3的系数,再根据x3的系数为a,二项式系数为b,求得a、b的值,可得
的值.
| a |
| b |
解答:
解:(x-
)6的展开式的展开式通项公式为Tk+1=
x6-k(-2x-
)k=(-2)k
x6-
k,
令6-
k=3,得k=2,即T3+1=(-2)2
x3=60x3即系数为a=60,
二项式系数为b=
=15,则
=4,
故答案为:4.
| 2 | ||
|
| C | k 6 |
| 1 |
| 2 |
| C | k 6 |
| 3 |
| 2 |
令6-
| 3 |
| 2 |
| C | 2 6 |
二项式系数为b=
| C | 2 6 |
| a |
| b |
故答案为:4.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
命题p:?t∈R,使得直线x-y+t=0与圆x2+y2=1相交;命题q:?m>0,双曲线
-
=1的离心率为
.
则下面结论正确的是( )
| x2 |
| m2 |
| y2 |
| m2 |
| 2 |
则下面结论正确的是( )
| A、p是假命题 |
| B、¬q是真命题 |
| C、p∧q是假命题 |
| D、p∧q是真命题 |
复数
的共轭复数对应的点位于( )
| 1-i |
| 2-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数y=f(x)的定义域为{x|x∈R,且x≠2},且y=f(x+2)是偶函数,当x<2时,f(x)=|2x-1|,那么当x>2时,函数f(x)的递减区间是( )
| A、(3,5) |
| B、(3,+∞) |
| C、(2,+∞) |
| D、(2,4] |
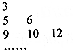 设{an}是集合{2s+2t|0≤s<t,且s、t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列{an}中的各项按照上小下大、左小右大的原则写成如图所示的三角形数阵,则a99=
设{an}是集合{2s+2t|0≤s<t,且s、t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列{an}中的各项按照上小下大、左小右大的原则写成如图所示的三角形数阵,则a99=