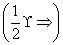题目内容
已知函数f(x)=loga(3-ax).
(1)当x∈[0,2]时,函数f(x)恒有意义,求实数a的取值范围.
(2)是否存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1?如果存在,试求出a的值;如果不存在,请说明理由.
解析 (1)由题意,3-ax>0对一切x∈[0,2]恒成立,∵a>0且a≠1,
∴g(x)=3-ax在[0,2]上是减函数,从而g(2)=3-2a>0得a< .∴a的取值范围为(0,1)∪
.∴a的取值范围为(0,1)∪ .
.
(2)假设存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1.
由题设f(1)=1,即loga(3-a)=1,
∴a= ,此时f(x)=log
,此时f(x)=log
 ,当x=2时,函数f(x)没有意义,故这样的实数a不存在.
,当x=2时,函数f(x)没有意义,故这样的实数a不存在.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

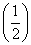 x-2的图象的交点为(x0,y0),则x0所在的区间是( ).
x-2的图象的交点为(x0,y0),则x0所在的区间是( ). ,则
,则 的定义域为( )
的定义域为( ) B.
B. C.
C. D.
D.
 则f(log23)=________.
则f(log23)=________. 的图象与函数y=2sin πx(-2≤x≤4)的图象所有交点的横坐标之和等于( ).
的图象与函数y=2sin πx(-2≤x≤4)的图象所有交点的横坐标之和等于( ).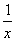 的单调增区间为( ).
的单调增区间为( ).