题目内容
已知tanx=2,则
的值为( )
| sin2x+1 |
| sin2x |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:原式利用同角三角函数间基本关系及二倍角的正弦函数化简,把tanx的值代入计算即可求出值.
解答:
解:∵tanx=2,
∴原式=
=
=
=
.
故选:A.
∴原式=
| 2sin2x+cos2x |
| 2sinxcosx |
| 2tan2x+1 |
| 2tanx |
| 2×4+1 |
| 2×2 |
| 9 |
| 4 |
故选:A.
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
球的半径是5,则它的体积是( )
| A、400π | ||
| B、100π | ||
C、
| ||
D、
|
为了得到函数y=cos(x+
)的图象,只需要把函数y=cos(x-
)的图象上的所有点( )
| π |
| 4 |
| π |
| 4 |
A、向右平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向左平行移动
|
已知集合A={x|-2<x<7},B={x|m+1<x<2m-1},且B≠∅,若A∪B=A,则( )
| A、-3≤m≤4 |
| B、-3<m<4 |
| C、2<m<4 |
| D、2<m≤4 |
若
(3x2+kx)dx=3,则k=( )
| ∫ | 1 0 |
| A、1 | B、2 | C、3 | D、4 |
一个三角形的三边长依次是4、6、2
,这个三角形的面积等于( )
| 7 |
A、3
| ||
B、6
| ||
C、3
| ||
D、6
|
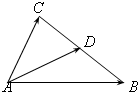
如图,已知△ABC中,D为BC边上的中点,则下列等式中正确的是( )

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
设f(x)是一次函数,f(8)=15,f(2),f(5),f(14)成等比数列,令Sn=f(1)+f(2)+f(3)+…+f(n),则Sn等于( )
| A、n2 |
| B、n2-n |
| C、n2+n |
| D、以上都不对 |