题目内容
S=1+2x+3x2+4x3+…+nxn-1（x≠0且x≠1）= ．
考点：数列的求和
专题：等差数列与等比数列
分析：直接利用错位相减法求数列的和．
解答：
解：S=1+2x+3x2+4x3+…+nxn-1．
xS=x+2x2+3x3+…+nxn．
两式作差得：（1-x）S=1+x+x2+…+xn-1-nxn，
∵x≠1且x≠0，
∴（1-x）S=
-nxn，
则S=
-
．
故答案为：
-
．
xS=x+2x2+3x3+…+nxn．
两式作差得：（1-x）S=1+x+x2+…+xn-1-nxn，
∵x≠1且x≠0，
∴（1-x）S=
| 1-xn |
| 1-x |
则S=
| 1-xn |
| (1-x)2 |
| nxn |
| 1-x |
故答案为：
| 1-xn |
| (1-x)2 |
| nxn |
| 1-x |
点评：本题考查了错位相减法求数列的和，关键是注意末项的符号，是中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
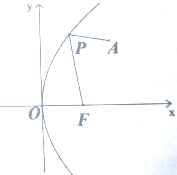如图，F是抛物线C：y2=2px的焦点，点A（4，2）为抛物线于内一点，点P为抛物线上一动点，|PA|+|PF|的最小值为8