题目内容
7.4名同学甲、乙、丙、丁按任意次序站成一排,甲或乙站在边上的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
分析 先求出甲、乙、丙、丁四人并排站成一排的事件种数,然后求出甲和乙站在中间的情况,从而求出甲或乙站在边上的情况,最后利用古典概型的概率公式进行求解即可.
解答 解:甲、乙、丙、丁四人并排站成一排一共有A44=24种
甲和乙站在中间的情况有A22•A22=4种
∴甲或乙站在边上的情况有20种
甲或乙站在边上的概率为 $\frac{20}{24}$=$\frac{5}{6}$,
故选:B.
点评 本题求的是概率实际上本题考查的是排列问题,把排列问题包含在实际问题中,解题的关键是看清题目的实质,把实际问题转化为数学问题,解出结果以后再还原为实际问题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
20.曲线的极坐标方程为ρ=2cosθ,则曲线的直角坐标方程为( )
| A. | (x-1)2+y2=1 | B. | x2+(y-1)2=1 | C. | (x-2)2+y2=1 | D. | x2+(y-2)2=1 |
2.定义在R上的函数f(x)的图象关于点(-$\frac{3}{4}$,0)成中心对称,且对任意的实数x都有$f(x)=-f(x+\frac{3}{2})$,f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2 017)=( )
| A. | 0 | B. | -2 | C. | 1 | D. | -4 |
16.已知A(-1,0),B(3,0),则与A距离为1且与B距离为4的点有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
17.若函数f(x)在其定义域的一个子集[a,b]上存在实数m(a<m<b),使f(x)在m处的导数f'(m)满足f(b)-f(a)=f'(m)(b-a),则称m是函数f(x)在[a,b]上的一个“中值点”,函数$f(x)=\frac{1}{3}{x^3}-{x^2}$在[0,b]上恰有两个“中值点”,则实数b的取值范围是( )
| A. | $(\frac{2}{3},3)$ | B. | (3,+∞) | C. | $(\frac{3}{2},3)$ | D. | $({\frac{3}{2},3}]$ |
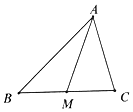 如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.
如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.