题目内容

17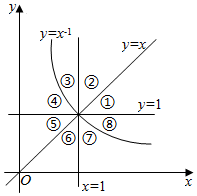．如图，函数$y=\frac{1}{x}$、y=x、y=1的图象和直线x=1将平面直角坐标系的第一象限分成八个部分：①②③④⑤⑥⑦⑧．若幂函数f（x）的图象经过的部分是④⑧，则f（x）可能是（　　）
A．y=x2B．$y=\frac{1}{{\sqrt{x}}}$C．$y={x^{\frac{1}{2}}}$D．y=x-2

分析 根据幂函数的图象和性质，进行分析判定即可．

解答 解：∵函数y=xα的图象过④⑧部分，
∴函数y=xα在第一象限内单调递减，
∴α＜0；
又x=2时，y=$\frac{1}{\sqrt{2}}$＞$\frac{1}{2}$，
∴函数y=xα的图象经过⑧部分，
∴取α=-$\frac{1}{2}$，
即函数y=${x}^{-\frac{1}{2}}$=$\frac{1}{\sqrt{x}}$．
故选：B．

点评 本题考查了幂函数的图象和性质，根据幂函数的图象与性质，利用数形结合的方法是解题的关键．

练习册系列答案
相关题目
7．已知$\overrightarrow{a}$=（2，m），$\overrightarrow{b}$=（-1，m），若（2$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{b}$，则|$\overrightarrow{a}$|=（　　）
A．2B．3C．4D．5
8．已知平面向量$\overrightarrow{a}$=（2，1），$\overrightarrow{c}$=（1，-1），若向量$\overrightarrow{b}$满足（$\overrightarrow{a}$-$\overrightarrow{b}$）∥$\overrightarrow{c}$，（$\overrightarrow{a}$+$\overrightarrow{c}$）⊥$\overrightarrow{b}$，则向量$\overrightarrow{b}$=（　　）
A．（2，1）B．（1，2）C．（3，0）D．（0，3）
5．已知tanα=-$\frac{3}{4}$，且tan（α+β）=1，则tanβ的值为（　　）
A．-7B．7C．-$\frac{3}{4}$D．$\frac{3}{4}$
12．已知函数$f（x）=cos2x+\sqrt{3}sin2x$，在下列四个命题中：
①函数的表达式可以改写为$f（x）=2cos（2x-\frac{π}{3}）$；
②当$x=kπ+\frac{π}{6}$（k∈Z）时，函数取得最大值为2；
③若x1≠x2，且f（x1）=f（x2）=0，则${x_1}-{x_2}=\frac{kπ}{2}（k∈Z且k≠0）$；
④函数f（x）的图象关于直线$x=\frac{2π}{3}$对称；
其中正确命题的序号是①②③④（把你认为正确命题的序号都填上）．
2．圆心为（1，-2），半径为4的圆的方程是（　　）
A．（x+1）2+（y-2）2=16B．（x-1）2+（y+2）2=16C．（x+1）2+（y-2）2=4D．（x-1）2+（y+2）2=4
9．已知函数$f（x）={log_{\frac{1}{2}}}（{x^2}-2ax+3）$．
（1）若函数的定义域为R，求实数a的取值范围；
（2）若函数的值域为（-∞，-1]，求实数a的取值范围；
（3）若函数在区间$（\frac{1}{2}，1）$上为增函数，求实数a的取值范围．
6．已知直线l的参数方程为$\left\{\begin{array}{l}{x=1+2t}\\{y=\frac{1}{2}-t}\end{array}\right.$，曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=sinθ}\end{array}\right.$，设直线l与曲线C交于两点A，B
（1）将直线1和曲线C化为普通方程；
（2）若P（1，$\frac{1}{2}$），求|PA|+|PB|，及|PA|•|PB|的值．
7．已知函数y=1+2sinxcosx．
（1）求函数的最小正周期；
（2）当x∈[-$\frac{π}{2}$，$\frac{π}{6}$]时，求最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网