题目内容
设Sn表示数列{an}的前n项和.
(1)若{an}为等差数列,推导Sn的计算公式;
(2)若a1=1,q≠0,且对所有正整数n,有Sn=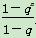 ,判断{an}是否为等比数列,并证明你的结论.
,判断{an}是否为等比数列,并证明你的结论.
解 (1)方法一:设{an}的公差为d,则Sn=a1+a2+…+an=a1+(a1+d)+…+[a1+(n-1)d],
又Sn=an+(an-d)+…+[an-(n-1)d],
∴2Sn=n(a1+an),∴Sn=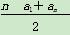 .
.
方法二:设{an}的公差为d,则Sn=a1+a2+…+an=a1+(a1+d)+…+[a1+(n-1)d],
又Sn=an+an-1+…+a1=[a1+(n-1)d]+[a1+(n-2)d]+…+a1,
∴2Sn=[2a1+(n-1)d]+[2a1+(n-1)d]+…+[2a1+(n-1)d]=2na1+n(n-1)d,
∴Sn=na1+ d.
d.
(2){an}是等比数列.证明如下:
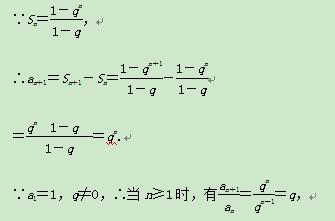 因此,{an}是首项为1且公比为q的等比数列.
因此,{an}是首项为1且公比为q的等比数列.

练习册系列答案
相关题目
 ,则满足an+1<an的n的取值为( )
,则满足an+1<an的n的取值为( )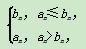 若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是________.
若在数列{cn}中,c5≤cn对任意n∈N*恒成立,则实数k的取值范围是________.
 n(4n2-1).
n(4n2-1). 所确定的平面区域内的动点,Q是直线2x+y=0上任意一点,O为坐标原点,则|
所确定的平面区域内的动点,Q是直线2x+y=0上任意一点,O为坐标原点,则|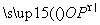 +
+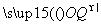 |的最小值为( )
|的最小值为( )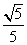 B.
B.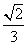
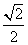 D.1
D.1