题目内容
11.某中学在高三年级开设大学先修课程(线性代数),共有50名同学选修,其中男同学30名,女同学20名.为了对这门课程的数学效果进行评估,学校按性别分别采用分成抽样的方法抽取5人进行考核.(1)求抽取的5人中男、女同学的人数;
(2)考核的第一轮是答辩,顺序由已抽取的甲、乙等5位同学按抽签方式决定.设甲、乙两位同学间隔的人数为X,X的分布列为
| X | 3 | 2 | 1 | 0 |
| P | $\frac{1}{10}$ | b | $\frac{3}{10}$ | a |
(3)考核的第二轮是笔试:5位同学的笔试成绩分别为115,122,105,111,109;结合第一轮的答辩情况,他们的考核成绩分别为125,132,115,121,119.这5位同学笔试成绩与考核成绩的方差分别记为s12,s22,试比较s12与s22的大小.(只需写出结论)
分析 (1)由分层抽样的性质,能求出抽取的5人中男、女同学的人数.
(2)由题意可得a=P(X=3)═,从而b=,由此能求出数学期望EX.
(3)由两组数据中相对应的数字之差均为10,得到${{s}_{1}}^{2}$=${{s}_{2}}^{2}$.
解答 解:(1)由分层抽样的性质得:
抽取的5人中男同学的人数为$\frac{5}{50}$×30=3,
女同学的人数为$\frac{5}{50}$×20=2.
(2)由题意可得:P(X=0)=$\frac{{2A}_{4}^{4}}{{A}_{5}^{5}}$=$\frac{2}{5}$.
即a=$\frac{2}{5}$,
因为a+b+$\frac{1}{10}$+$\frac{3}{10}$=1,
所以 b=$\frac{1}{5}$.
所以EX=3×$\frac{1}{10}$+2×$\frac{1}{5}$+1×$\frac{3}{10}$+0×$\frac{2}{5}$=1.
(3)${{s}_{1}}^{2}$=${{s}_{2}}^{2}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
1.调查某桑场采桑员和辅助工关于桑毛虫皮炎发病情况结果如表:
(1)完成2×2列联表;
(2)利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?
(参考公式:χ2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 采桑 | 不采桑 | 合计 | |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 |
(2)利用2×2列联表的独立性检验估计,“患桑毛虫皮炎病与采桑”是否有关?
| 参考数据 | 当χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当χ2>2.706时,有90%把握判定变量A,B有关联; | |
| 当χ2>3.841时,有95%把握判定变量A,B有关联; | |
| 当χ2>6.635时,有99%把握判定变量A,B有关联. |
2.有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次,根据年龄将大众评委分为5组,各组的人数如表:
(1)为了调查评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从E组中抽取了8人.请将其余各组抽取的人数填入如表.
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,设每位评委支持歌手不相互影响,求这2人至少有1人支持1号歌手的概率.
| 组别 | A | B | C | D | E |
| 人数 | 50 | 50 | 150 | 150 | 100 |
| 组别 | A | B | C | D | E |
| 人数 | 50 | 50 | 150 | 150 | 100 |
| 抽取人数 | 8 |
19.等比数列-3,-6,…的第四项等于( )
| A. | -24 | B. | -9 | C. | -12 | D. | 24 |
6.若向量$\overrightarrow a$=(-2,3),$\overrightarrow b$=(4,m),已知向量$\overrightarrow a$∥$\overrightarrow b$,则实数m=( )
| A. | 8 | B. | -8 | C. | 6 | D. | -6 |
14.已知函数y=x3-ax2-3x+b在x=1处取得极值2,则实数a,b的值分别为( )
| A. | 0和-4 | B. | 0;b取任意实数 | C. | 0和4 | D. | 4;b取任意实数 |
15.函数f(x)=x3-12x的极小值点是( )
| A. | 2 | B. | -2 | C. | -16 | D. | 16 |
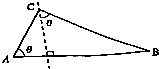 某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.
某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.