题目内容
已知一条确定线段AB与平面α成60°角，点A、点C在平面α内，若△ABC面积一定，证明：点C的运动轨迹是椭圆．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由已知条件推导出点C到线段AB的距离不变，由此得到点C在以AB为轴的圆柱体的侧面上，从而能够证明点C的运动轨迹是椭圆．
解答：
证明：∵一条确定线段AB与平面α成60°角，
点A、点C在平面α内，且△ABC面积一定，
∴点C到线段AB的距离不变，
∴点C在以AB为轴的圆柱体的侧面上，
由一条确定线段AB与平面α成60°角，
知这个以AB为轴的圆柱体与平面α相交但不垂直，
∴点C的运动轨迹是椭圆．
点A、点C在平面α内，且△ABC面积一定，
∴点C到线段AB的距离不变，
∴点C在以AB为轴的圆柱体的侧面上，
由一条确定线段AB与平面α成60°角，
知这个以AB为轴的圆柱体与平面α相交但不垂直，
∴点C的运动轨迹是椭圆．
点评：本题考查点的运动轨迹是椭圆的证明，是中档题，解题时要认真审题，要熟练掌握椭圆概念．
练习册系列答案
相关题目
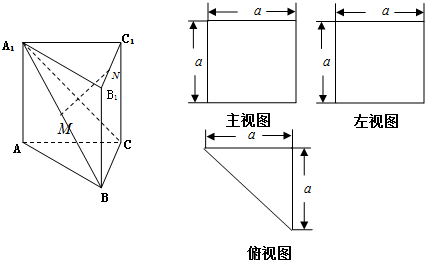一个多面体的直观图、主视图、左视图、俯视图如图，M、N分别为A1B、B1C1的中点．下列结论中正确的个数有（ ）