题目内容
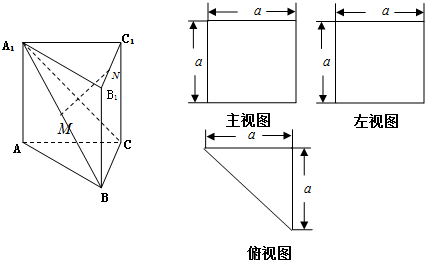 一个多面体的直观图、主视图、左视图、俯视图如图,M、N分别为A1B、B1C1的中点.下列结论中正确的个数有( )
一个多面体的直观图、主视图、左视图、俯视图如图,M、N分别为A1B、B1C1的中点.下列结论中正确的个数有( )①直线MN与A1C相交.
②MN⊥BC.
③MN∥平面ACC1A1.
④三棱锥N-A1BC的体积为VN-A1BC=
| 1 |
| 6 |
| A、4个 | B、3个 | C、2个 | D、1个 |
考点:简单空间图形的三视图
专题:空间位置关系与距离
分析:根据直线MN与A1C是异面直线,可判定①错误;
连接AC1,交A1C于O,连接OM,证明MN∥OC1,可证MN∥平面ACC1A1,③正确;
再证BC⊥平面ACC1A1,OC1?平面ACC1A1,从而证明BC⊥OC1,故MN⊥BC,②正确;
根据VN-A1BC=VA1-BCN=
×
×a×a×a=
a3.可得④正确.
连接AC1,交A1C于O,连接OM,证明MN∥OC1,可证MN∥平面ACC1A1,③正确;
再证BC⊥平面ACC1A1,OC1?平面ACC1A1,从而证明BC⊥OC1,故MN⊥BC,②正确;
根据VN-A1BC=VA1-BCN=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
解答:
解:∵直线MN与A1C是异面直线,∴①错误;
如图连接AC1,交A1C于O,连接OM,∵M、O分别是BA1、CA1的中点,
∴OM∥BC,OM=
BC,又BC∥B1C1,BC=B1C1,N为B1C1的中点,
∴OM∥NC1,OM=NC1,∴四边形OMNC1为平行四边形,∴MN∥OC1,
BC⊥AC,∴BC⊥平面ACC1A1,OC1?平面ACC1A1,∴BC⊥OC1,
∴MN⊥BC,②正确;
又MN?平面ACC1A1,BC?平面ACC1A1,∴MN∥平面ACC1A1,③正确;
∵A1C1⊥平面BCC1B1,∴A1C1为三棱锥A1-BCN的高,
∴VN-A1BC=VA1-BCN=
×
×a×a×a=
a3.∴④正确.
故选:B.
如图连接AC1,交A1C于O,连接OM,∵M、O分别是BA1、CA1的中点,
∴OM∥BC,OM=
| 1 |
| 2 |
∴OM∥NC1,OM=NC1,∴四边形OMNC1为平行四边形,∴MN∥OC1,
BC⊥AC,∴BC⊥平面ACC1A1,OC1?平面ACC1A1,∴BC⊥OC1,
∴MN⊥BC,②正确;
又MN?平面ACC1A1,BC?平面ACC1A1,∴MN∥平面ACC1A1,③正确;
∵A1C1⊥平面BCC1B1,∴A1C1为三棱锥A1-BCN的高,
∴VN-A1BC=VA1-BCN=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故选:B.
点评:本题考查了线面垂直的判定与性质,线面平行的判定及棱锥的体积计算,考查了学生的空间想象能力与推理论证能力.

练习册系列答案
相关题目
设集合A={x|2≤x≤6},B={x|a≤x≤a+3},若B⊆A,则实数a的取值范围是( )
| A、{a|2≤a≤3} |
| B、{a|a≥3} |
| C、{a|a≥2} |
| D、{a|1<a<3} |
已知复数Z=(1+i)(2-i)的实部是m,虚部是n,则m•n的值是( )
| A、3 | B、-3 | C、3i | D、-3i |