题目内容
18．不等式x（1-x）＞0的解集为（ ）| A． | （-1，0） | B． | （-∞，-1）∪（0，+∞） | C． | （0，1） | D． | （-∞，0）∪（1，+∞） |
分析 由已知将不等式等价化为x（x-1）＜0，求出不等式的解集．
解答 解：由已知，不等式等价于x（x-1）＜0，所以不等式的解集为：{x|0＜x＜1}；
故选C．
点评 本题考查了一元二次不等式的解法；等价将不等式化为二次项系数为正数，然后根据二次不等式与二次函数的关系，求出不等式的解集．属于基础题．
练习册系列答案
相关题目
8．已知平面向量$\overrightarrow{a}$=（1，x），$\overrightarrow{b}$=（x-1，2），若$\overrightarrow{a}$与$\overrightarrow{b}$共线且方向相同，则x=（ ）
| A． | 1 | B． | 2 | C． | -1 | D． | -2 |
6．如图是一个几何体的三视图，则该几何体的表面积为（ ）
| A． | 46 | B． | 48 | C． | 50 | D． | 52 |
13．下列函数中，既是偶函数又在区间 （0，+∞）上单调递减的是（ ）
| A． | y=$\frac{1}{x}$ | B． | y=e-x | C． | y=-x2+1 | D． | y═lg|x| |
3．实数a，b，c满足a+b+c=3，ab+2c=6，则实数c的取值范围是（ ）
| A． | （-∞，-5]∪[3，+∞） | B． | [-5，3] | C． | （-∞，-3]∪[5，+∞） | D． | [-3，5] |
6．已知曲线C1：y=sinx，C2：y=sin（2x+$\frac{2π}{3}$），则下面结论正确的是（ ）
| A． | 把C1上各点的横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变，再把得到的曲线向左平移$\frac{2π}{3}$个单位长度，得到曲线C2 | |
| B． | 把C1上各点的横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变，再把得到的曲线向左平移$\frac{π}{3}$个单位长度，得到曲线C2 | |
| C． | 把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移$\frac{2π}{3}$个单位长度，得到曲线C2 | |
| D． | 把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个$\frac{π}{3}$单位长度，得到曲线C2 |
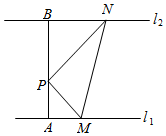如图，P是两条平行直线l1，l2之间的一个定点，且点P到l1，l2的距离分别为PA=1，PB=$\sqrt{3}$，设△PMN的另两个顶点M，N分别在l1，l2上运动，设∠MPN=α，∠PMN=β，∠PNM=γ，且满足sinβ+sinγ=sinα（cosβ+cosγ）．