题目内容
15.已知函数f(x)=|x-1|+|x+2|(Ⅰ)作出函数f(x)的图象(不要求写作法);
(Ⅱ)若不等式9a2+1≥|a|f(x)对a∈(-∞,0)∪(0,+∞)恒成立,求实数x的取值范围.
分析 (Ⅰ)运用分段函数的形式写出f(x),再由分段函数的画法,可得图象;
(Ⅱ)由题意可得f(x)≤9|a|+$\frac{1}{|a|}$的最小值,运用基本不等式求得右边函数的最小值,再由绝对值不等式的解法,即可得到所求范围.
解答 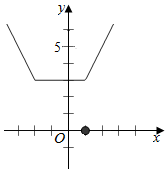 解:(Ⅰ)f(x)=$\left\{\begin{array}{l}{2x+1,x≥1}\\{3,-2<x<1}\\{-1-2x,x≤-2}\end{array}\right.$,
解:(Ⅰ)f(x)=$\left\{\begin{array}{l}{2x+1,x≥1}\\{3,-2<x<1}\\{-1-2x,x≤-2}\end{array}\right.$,
作出函数f(x)的图象,如右:
(Ⅱ)不等式9a2+1≥|a|f(x)对a∈(-∞,0)∪(0,+∞)恒成立,
即有f(x)≤9|a|+$\frac{1}{|a|}$的最小值,
由9|a|+$\frac{1}{|a|}$≥2$\sqrt{9|a|•\frac{1}{|a|}}$=6,当且仅当|a|=$\frac{1}{3}$取得最小值6.
即有|x-1|+|x+2|≤6,
即为$\left\{\begin{array}{l}{2x+1≤6}\\{x≥1}\end{array}\right.$或$\left\{\begin{array}{l}{3≤6}\\{-2<x<1}\end{array}\right.$或$\left\{\begin{array}{l}{-1-2x≤6}\\{x≤-2}\end{array}\right.$,
即为1≤x≤$\frac{5}{2}$或-2<x<-1或-$\frac{7}{2}$≤x≤-2,
解得-$\frac{7}{2}$≤x≤$\frac{5}{2}$.
则实数x的取值范围为[-$\frac{7}{2}$,$\frac{5}{2}$].
点评 本题考查绝对值函数的图象的画法,考查不等式恒成立问题的解法,注意转化为求函数的最值,运用基本不等式,同时考查绝对值不等式的解法,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (-3,log29) | B. | (-3,4) | C. | (-∞,log29) | D. | (-∞,4) |
| A. | sinx+$\frac{1}{sinx}$≥2 | B. | x2+4≥4|x| | C. | lg(x2+1)>lg(2x) | D. | $\frac{1}{a}$+$\frac{1}{b}$>$\frac{2}{\sqrt{ab}}$ |
| A. | 4 | B. | 0 | C. | -1 | D. | 1 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 9 | B. | 8 | C. | 7 | D. | 2 |