题目内容
4．甲抛掷均匀硬币2017次，乙抛掷均匀硬币2016次，下列四个随机事件的概率是0.5的是（ ）①甲抛出正面次数比乙抛出正面次数多；
②甲抛出反面次数比乙抛出正面次数少；
③甲抛出反面次数比甲抛出正面次数多；
④乙抛出正面次数与乙抛出反面次数一样多．
| A． | ①② | B． | ①③ | C． | ②③ | D． | ②④ |
分析 甲抛掷均匀硬币2017次，乙抛掷均匀硬币2016次，每次抛掷时出现正面的概率都是0.5，出现反面的概率也都是0.5，由此能求出结果．
解答 解：根据题意，甲抛掷均匀硬币2017次，乙抛掷均匀硬币2016次，
每次抛掷时出现正面的概率都是0.5，出现反面的概率也都是0.5，
在①中，∵甲比乙多抛掷一次硬币，∴甲抛出正面次数比乙抛出正面次数多的概率为0.5，故①正确；
在②中，∵甲比乙多抛掷一次硬币，∴甲抛出反面次数比乙抛出正面次数少的概率不是0.5，故②错误；
在③中，∵甲抛掷均匀硬币2017次，∴甲抛出反面次数比甲抛出正面次数多的概率是0.5，故③正确；
在④中，∵乙抛掷均匀硬币2016次，
∴乙抛出正面次数与乙抛出反面次数一样多的概率为${C}_{2016}^{1008}（\frac{1}{2}）^{1008}（\frac{1}{2}）^{1008}$，故④错误．
故选：B．
点评 本题考查命题真假的判断，是基础题，解题时要认真审题，注意概率的意义的合理运用．
练习册系列答案
相关题目
15．某种产品的年销售量y与该年广告费用支出x有关，现收集了4组观测数据列于下表：
现确定以广告费用支出x为解释变量，销售量y为预报变量对这两个变量进行统计分析．
（1）已知这两个变量满足线性相关关系，试建立y与x之间的回归方程；
（2）假如2014年广告费用支出为10万元，请根据你得到的模型，预测该年的销售量y．
（3）根据公式R2=1-$\frac{\sum_{i=1}^{n}（{y}_{i}-\widehat{{y}_{i}}）^{2}}{\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}$，计算相关指数R2．
| x（万元） | 1 | 4 | 5 | 6 |
| y（万元） | 30 | 40 | 60 | 50 |
（1）已知这两个变量满足线性相关关系，试建立y与x之间的回归方程；
（2）假如2014年广告费用支出为10万元，请根据你得到的模型，预测该年的销售量y．
（3）根据公式R2=1-$\frac{\sum_{i=1}^{n}（{y}_{i}-\widehat{{y}_{i}}）^{2}}{\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}$，计算相关指数R2．
12．通过随机询问200名性别不同的大学生是否爱好踢毽子运动，计算得到统计量K2的观测值k≈4.892，参照附表，得到的正确结论是（ ）
| P（K2≥k） | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A． | 有97.5%以上的把握认为“爱好该项运动与性别有关” | |
| B． | 有97.5%以上的把握认为“爱好该项运动与性别无关” | |
| C． | 在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别有关” | |
| D． | 在犯错误的概率不超过5%的前提下，认为“爱好该项运动与性别无关” |
19．某学校共有教职工900人，分成三个批次进行继续教育培训，在三个批次中男、女教职工人数如下表所示，其中第二批次女教职工人数占总人数的16%．
（1）求x的值；
（2）现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查，问应在第三批次中抽取教职工多少名？
| 第一批次 | 第二批次 | 第三批次 | |
| 女教职工 | 196 | x | y |
| 男教职工 | 204 | 156 | z |
（2）现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查，问应在第三批次中抽取教职工多少名？
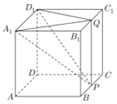如图，正方体ABCD-A1B1C1D1中，AB=4，P、Q分别是棱BC与B1C1的中点．
，则下列不等式成立的是 （ ）
B．
D．