题目内容
12.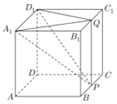 如图,正方体ABCD-A1B1C1D1中,AB=4,P、Q分别是棱BC与B1C1的中点.
如图,正方体ABCD-A1B1C1D1中,AB=4,P、Q分别是棱BC与B1C1的中点.(1)求异面直线D1P和A1Q所成角的大小;
(2)求以A1、D1、P、Q四点为四个顶点的四面体的体积.
分析 (1)以D为原点,DA,DC,DD1为x,y,z轴,建立空间直角坐标系,利用向量法能求出异面直线D1P和A1Q所成角.
(2)以A1、D1、P、Q四点为四个顶点的四面体的体积V=$\frac{1}{3}×{S}_{△{A}_{1}{D}_{1}Q}×PQ$.
解答 解:(1)以D为原点,DA,DC,DD1为x,y,z轴,建立空间直角坐标系,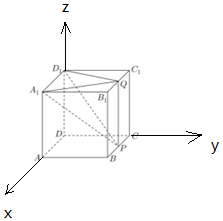
则D1(0,0,4),P(2,4,0),A1(4,0,4),Q(2,4,4),
$\overrightarrow{{D}_{1}P}$=(2,4,-4),$\overrightarrow{{A}_{1}Q}$=(-2,4,0),
设异面直线D1P和A1Q所成角为θ,
则cosθ=$\frac{|\overrightarrow{{D}_{1}P}•\overrightarrow{{A}_{1}Q}|}{|\overrightarrow{{D}_{1}P}|•|\overrightarrow{{A}_{1}Q}|}$=$\frac{12}{\sqrt{36}•\sqrt{20}}$=$\frac{\sqrt{5}}{5}$,
∴θ=arccoa$\frac{\sqrt{5}}{5}$.
∴异面直线D1P和A1Q所成角为arccos$\frac{\sqrt{5}}{5}$.
(2)∵${S}_{△{A}_{1}{D}_{1}Q}$=$\frac{1}{2}×4×4$=8,PQ⊥平面A1D1Q,且PQ=4,
∴以A1、D1、P、Q四点为四个顶点的四面体的体积:
V=$\frac{1}{3}×{S}_{△{A}_{1}{D}_{1}Q}×PQ$=$\frac{1}{3}×8×4$=$\frac{32}{3}$.
点评 本题考查异面直线所成角的求法,考查四面体的体积的求法,是中档题,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案①甲抛出正面次数比乙抛出正面次数多;
②甲抛出反面次数比乙抛出正面次数少;
③甲抛出反面次数比甲抛出正面次数多;
④乙抛出正面次数与乙抛出反面次数一样多.
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
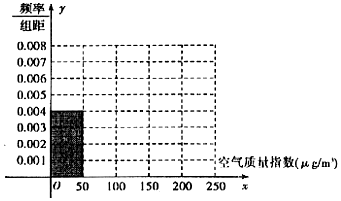
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为51-100和151-200的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
| A. | (0,2] | B. | (1,2] | C. | [1,2] | D. | [1,4] |
| A. | -4或16 | B. | 20 | C. | -4或20 | D. | -4 |
 中,
中, ,点
,点 是
是 的中点.
的中点.
 ;
; 平面
平面 .
.